��Ŀ����
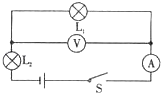
����Ŀ����ͼ��ij�����豸�IJ��ֵ�·����Դ��ѹU=4.5V���ֲ��䣬����L���С�6V��6W����������֪�պϿ���S1��S3ʱ����·���ĵĹ���Ϊ2.025W�����Ƶ�˿�������¶ȵı仯��
��1����ֵ����R3����ֵ��
��2����������S1 �� S2 �� S3���պ�ʱ����ͨ���������ĵ�����С��
��3����ѹ��������Ϊ0��3V��������������Ϊ0��0.6A������������R2����ֵ��0��20���ڿɵ���ֻ�պϿ���S2 �� �ڱ�֤�����ȫ������£������L���ĵĵ繦�ʵı仯��Χ��
���𰸡�
��1��
�⣺�պϿ���S1��S2ʱ����·ΪR1�ļ�·��
��P= ![]() �ɵã���ֵ����R3����ֵ��
�ɵã���ֵ����R3����ֵ��
R3= ![]() =
= ![]() =10��
=10��
�𣺶�ֵ����R3����ֵΪ10����
��2��
��������S1��S2��S3���պ�ʱ��R1��L���������������·��·��
��P= ![]() �ɵã����ݵĵ��裺
�ɵã����ݵĵ��裺
RL= ![]() =
= ![]() =6����
=6����
������·���ܵ���ĵ������ڸ��ֵ��赹��֮�ͣ�
���ԣ���·�е��ܵ��裺
R= ![]() =
= ![]() =3.75����
=3.75����
ͨ���������ĵ�����С��
I= ![]() =
= ![]() =1.2A��
=1.2A��
����������S1��S2��S3���պ�ʱ��ͨ���������ĵ���Ϊ1.2A��
��3��
�⣺ֻ�պϿ���S2ʱ������L��R2���������������·�еĵ�·����ѹ����L���˵ĵ�ѹ��
���ݵĶ������
IL= ![]() =
= ![]() =1A��
=1A��
������·�и����ĵ�����ȣ��ҵ�����������Ϊ0��0.6A��
���ԣ���·�е�������I��=0.6A��
��������ĵ�����ʣ�
PL��=I��2RL=��0.6A��2��6��=2.16W��
����ѹ����ʾ�����U2=3Vʱ����·�еĵ�����С���������ĵĵ繦����С��
������·���ܵ�ѹ���ڸ��ֵ�ѹ֮�ͣ�
���ԣ��������˵ĵ�ѹ��
UL��=U��U2=4.5V��3V=1.5V��
����L���ĵ���С���ʣ�
PLС= ![]() =
= ![]() =0.375W��
=0.375W��
���ԣ�����L���ĵĵ繦�ʵı仯��Χ0.375W��2.16W��
��ֻ�պϿ���S2���ڱ�֤�����ȫ������£�����L���ĵĵ繦�ʵı仯��ΧΪ0.375W��2.16W��
����������1���պϿ���S1��S2ʱ����·ΪR1�ļ�·������P= ![]() �����ֵ����R3����ֵ����2����������S1 �� S2 �� S3���պ�ʱ��R1��L���������������·��·������P=
�����ֵ����R3����ֵ����2����������S1 �� S2 �� S3���պ�ʱ��R1��L���������������·��·������P= ![]() ������ݵĵ��裬�ٸ��ݵ���IJ��������·�е��ܵ��裬����ŷķ�������ͨ���������ĵ�����С����3��ֻ�պϿ���S2ʱ������L��R2���������������·�еĵ�·����ѹ����R2���˵ĵ�ѹ������ŷķ����������ݵĶ������Ȼ�����������������Ƚ�ȷ����·��������������P=I2R�������L���ĵ�����ʣ�����ѹ����ʾ�����ʱ��·�еĵ�����С���������ĵĵ繦����С�����ݴ�����·�ĵ�ѹ�ص�����������˵ĵ�ѹ������P=
������ݵĵ��裬�ٸ��ݵ���IJ��������·�е��ܵ��裬����ŷķ�������ͨ���������ĵ�����С����3��ֻ�պϿ���S2ʱ������L��R2���������������·�еĵ�·����ѹ����R2���˵ĵ�ѹ������ŷķ����������ݵĶ������Ȼ�����������������Ƚ�ȷ����·��������������P=I2R�������L���ĵ�����ʣ�����ѹ����ʾ�����ʱ��·�еĵ�����С���������ĵĵ繦����С�����ݴ�����·�ĵ�ѹ�ص�����������˵ĵ�ѹ������P= ![]() �������L���ĵ���С���ʣ�Ȼ��ó��𰸣����⿼���˴�������·���ص��ŷķ���ɡ��繦�ʹ�ʽ��Ӧ�ã��ؼ��ǿ��رպϡ��Ͽ�ʱ��·���ӷ�ʽ���ж��Լ����һ���е������������ʱ���жϣ�
�������L���ĵ���С���ʣ�Ȼ��ó��𰸣����⿼���˴�������·���ص��ŷķ���ɡ��繦�ʹ�ʽ��Ӧ�ã��ؼ��ǿ��رպϡ��Ͽ�ʱ��·���ӷ�ʽ���ж��Լ����һ���е������������ʱ���жϣ�
�����㾫�������ڱ��⿼���ŷķ���ɼ���Ӧ�ú͵繦�ʵļ��㹫ʽ����Ҫ�˽�ŷķ���ɵ�Ӧ�ã� �� ͬһ�����裬��ֵ���䣬������͵�ѹ�� ����������������˵ĵ�ѹ����ʱ��ͨ���ĵ���Ҳ����R=U/I�� �� ����ѹ����ʱ������Խ����ͨ���ĵ�����ԽС����I=U/R�� �� ������һ��ʱ������Խ����������˵ĵ�ѹ��Խ��U=IR��������繦�ʹ�ʽ��P =W/t ��P=UI ; ʽ�е�λP����(w)��W������t���룻U������V����I������A������繦�ʻ����ù�ʽ��P=I2R��P= U2/R���ܵó���ȷ�𰸣�

����Ŀ��Ϊ�˱Ƚ�ˮ��ʳ���͵�����������С����������ͬ��װ��������ͼ��ʾ��ʵ�飮���¶ȼƲ���Һ���������������ߵ��¶�ֵ�������ӱ���¼����ʱ�䣮ʵ�����ݼ�¼�����
���� | ����/g | ��ʼ�¶�/�� | ����ʱ��/min | ����¶�/�� |
ˮ | 60 | 20 | 6 | 45 |
ʳ���� | 60 | 20 | 6 | 68 |
��1����ʵ������п��Ƽ���ʱ����ͬ��ͨ���Ƚ����о�ˮ��ʳ�������������IJ��죮
��2���ڴ�ʵ���У����Ҫʹˮ��ʳ���͵�����¶���ͬ����Ҫ�����ȸ�����ʱ�䣬��ʱˮ���յ�������ѡ����ڡ���С�ڡ����ڡ���ʳ�������յ�������
��3��ͨ��ʵ����Եõ���ͬ����������������ͬ�����ʵ����������������������������