题目内容
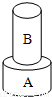
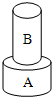
材料相同的两个圆柱体A、B，他们的底面半径为rA、rB，将它们分别放在水平桌面上，B对桌面的压强为p1．将B叠放在A上（如图所示），A对桌面的压强为p2，已知rA：rB=2：1，p1：p2=1：3，则两圆柱体的高度之比hA：hB为（ ）
| A．5：2 | B．11：4 | C．2：5 | D．4：11 |
设两圆柱体的密度为ρ，则A、B物体的重力：
GA=mAg=ρVAg=ρSAhAg，GB=mBg=ρVBg=ρSBhBg，
∵水平面上物体的压力和自身的重力相等，
∴B对桌面的压强：
p1=
=
=
=ρhBg，
B叠放在A上时，A对桌面的压力：
FA=GA+GB=ρASAhAg+ρBSBhBg，
A对桌面的压强：
p2=
=
=ρhAg+ρ
g，
∵S=πr2，且rA：rB=2：1，
∴
=
=（
）2=（
）2=
，
∵p1：p2=1：3，
∴3ρhBg=ρhAg+ρ
g=ρhAg+ρ
g=ρhAg+
ρhBg，
解得：
=
．
故选B．
GA=mAg=ρVAg=ρSAhAg，GB=mBg=ρVBg=ρSBhBg，
∵水平面上物体的压力和自身的重力相等，
∴B对桌面的压强：
p1=
| FB |
| SB |
| GB |
| SB |
| ρSBhBg |
| SB |
B叠放在A上时，A对桌面的压力：
FA=GA+GB=ρASAhAg+ρBSBhBg，
A对桌面的压强：
p2=
| FA |
| SA |
| ρSAhAg+ρSBhBg |
| SA |
| SBhB |
| SA |
∵S=πr2，且rA：rB=2：1，
∴
| SA |
| SB |
| πrA2 |
| πrB2 |
| rA |
| rB |
| 2 |
| 1 |
| 4 |
| 1 |
∵p1：p2=1：3，
∴3ρhBg=ρhAg+ρ
| SBhB |
| SA |
| SBhB |
| 4SB |
| 1 |
| 4 |
解得：
| hA |
| hB |
| 11 |
| 4 |
故选B．
练习册系列答案
英才计划期末调研系列答案
相关题目
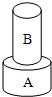（2007?丰台区一模）材料相同的两个圆柱体A、B，他们的底面半径为rA、rB，将它们分别放在水平桌面上，B对桌面的压强为p1．将B叠放在A上（如图所示），A对桌面的压强为p2，已知rA：rB=2：1，p1：p2=1：3，则两圆柱体的高度之比hA：hB为（ ）
如图所示，同种材料组成的高度相同、体积不同的两个圆柱体，已知它们的体积关系是V甲=2V乙，它们对桌面的压强之比是（ ）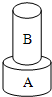
材料相同的两个圆柱体A、B，他们的底面半径为rA、rB，将它们分别放在水平桌面上，B对桌面的压强为p1．将B叠放在A上（如图所示），A对桌面的压强为p2，已知rA：rB=2：1，p1：p2=1：3，则两圆柱体的高度之比hA：hB为