题目内容
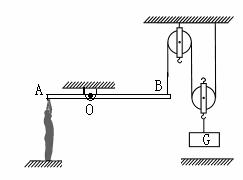
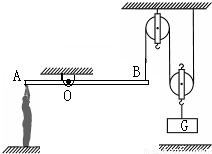
 如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N.(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg)
如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N.(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg)
求:(1)F1与F2之比;
(2)人的质量m人;
(3)当重物G被匀速提升过程中,滑轮组的机械效率η;
(4)已知重物G的密度与水的密度比为9:1,将重物完全浸没在水中匀速上升时的速度为0.1m/s,若此时已知动滑轮重为100N,那么绳端B的拉力F′做功的功率P′为多大?
解:(1)人的重力:G人=P0S
当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,则人对地面的压力
F2+G人=P2S,
∴F2+P0S=P2S,即:1500N=(5.75×104Pa-2×104Pa)S
∴S=0.04m2
当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,则人对地面的压力
F1+G人=P1S
∴F1=P1S-P0S=(2.375×104Pa-2×104Pa)×0.04m2=150N
故F1:F2=150N:1500N=1:10;
答:F1:F2=的比值为1:10.
(2)G人=P0S=2×104Pa×0.04m2=800N
人的质量m人= =
=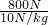 =80kg;
=80kg;
答:人的质量m人=80kg;
(3)当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,假设人使杠杆A端上升高度h,则F1做的功为W1=F1h,这时,因没有提升任何物体,所的功为额外功,
当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,假设人使杠杆A端上升高度h,则F2做的总功为W2=F2h,
故滑轮组的机械效率η=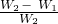 ×100%=
×100%=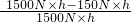 ×100%=90%;
×100%=90%;
答:当重物G被匀速提升过程中,滑轮组的机械效率η=90%
(4)当滑轮下未挂重物时,杠杆平衡,F1=150N,
右边的滑轮部分,因未挂重物,动滑轮重力为100N,则B端绳子的作用力FB′=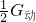 =
=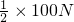 =50N,
=50N,
根据杠杆平衡条件知:F1OA=FB′OB,
∴ =
=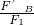 =
= =
= ,
,
当加挂重物后他对杠杆A端施加的举力为F2,B端绳子的作用力为FB″= ,则由杠杆平衡条件得:
,则由杠杆平衡条件得:
F2OA=FB″OB,即:F2OA= OB,
OB,
∴G=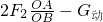 =
=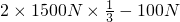 =900N,
=900N,
当将重物完全浸没在水中,重物对动滑轮的拉力
G′=G-F浮=G-ρ水gV物=G-ρ水g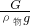 =G(1-
=G(1-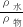 )=900N×(1-
)=900N×(1- )=800N,
)=800N,
所以,绳端B的拉力F′= (G′+G动)=
(G′+G动)= ×(800N+100N)=450N,速度为vB=2v=2×0.1m/s=0.2m/s,
×(800N+100N)=450N,速度为vB=2v=2×0.1m/s=0.2m/s,
功率P′=F′vB=450N×0.2m/s=90W.
答:绳端B的拉力F′做功的功率P′=90W.
分析:(1)知道两次用力时对地面的压强,分别列方程式求出当滑轮下未挂重物时,他对杠杆A端施加的举力分别为F1、人的重力和受力面积(与地的接触面积);
(2)再利用重力公式求人的质量;
(3)当滑轮下未挂重物时,他用力F1匀速举起杠杆的A端时所做的功为利用这个机械时的额外功,当滑轮下加挂重物G后,他用力F2匀速举起杠杆的A端所做的功为总功,根据机械效率的公式即可求整个滑轮组的机械效率η;
(4)根据滑轮下未挂重物时,动滑轮重力为100N,利用杠杆平衡求出力臂OA与OB的关系,再根据当加挂重物后他对杠杆A端施加的举力为F2,由杠杆平衡条件得出重物的重力,然后当将重物完全浸没在水中,根据重物受力情况求出对动滑轮的拉力G′,最后利用P=Fv即可求功率.
点评:本题考查压强的计算,注意分析出压强变化的原因,即可解答本题的杠杆A端的拉力和人的重力,正确理解在滑轮下未挂重物时,他用力匀速举起杠杆的A端所的功为整个机械的额外功,其实在杠杆、绳重和机械间摩擦忽略不计时,这个额外功就是对动滑轮所做的功,并在(4)问中结合动滑轮的重力,利用杠杆平衡条件得出杠杆的力臂关系,这是解答本题机械效率和绳端B的拉力F′的重要关键所在.本题难点太大.
当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,则人对地面的压力
F2+G人=P2S,
∴F2+P0S=P2S,即:1500N=(5.75×104Pa-2×104Pa)S
∴S=0.04m2
当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,则人对地面的压力
F1+G人=P1S
∴F1=P1S-P0S=(2.375×104Pa-2×104Pa)×0.04m2=150N
故F1:F2=150N:1500N=1:10;
答:F1:F2=的比值为1:10.
(2)G人=P0S=2×104Pa×0.04m2=800N
人的质量m人=
 =
=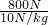 =80kg;
=80kg;答:人的质量m人=80kg;
(3)当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,假设人使杠杆A端上升高度h,则F1做的功为W1=F1h,这时,因没有提升任何物体,所的功为额外功,
当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,假设人使杠杆A端上升高度h,则F2做的总功为W2=F2h,
故滑轮组的机械效率η=
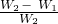 ×100%=
×100%=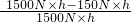 ×100%=90%;
×100%=90%;答:当重物G被匀速提升过程中,滑轮组的机械效率η=90%
(4)当滑轮下未挂重物时,杠杆平衡,F1=150N,
右边的滑轮部分,因未挂重物,动滑轮重力为100N,则B端绳子的作用力FB′=
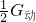 =
=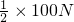 =50N,
=50N,根据杠杆平衡条件知:F1OA=FB′OB,
∴
 =
=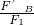 =
= =
= ,
,当加挂重物后他对杠杆A端施加的举力为F2,B端绳子的作用力为FB″=
 ,则由杠杆平衡条件得:
,则由杠杆平衡条件得:F2OA=FB″OB,即:F2OA=
 OB,
OB,∴G=
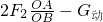 =
=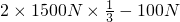 =900N,
=900N,当将重物完全浸没在水中,重物对动滑轮的拉力
G′=G-F浮=G-ρ水gV物=G-ρ水g
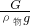 =G(1-
=G(1-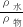 )=900N×(1-
)=900N×(1- )=800N,
)=800N,所以,绳端B的拉力F′=
 (G′+G动)=
(G′+G动)= ×(800N+100N)=450N,速度为vB=2v=2×0.1m/s=0.2m/s,
×(800N+100N)=450N,速度为vB=2v=2×0.1m/s=0.2m/s,功率P′=F′vB=450N×0.2m/s=90W.
答:绳端B的拉力F′做功的功率P′=90W.
分析:(1)知道两次用力时对地面的压强,分别列方程式求出当滑轮下未挂重物时,他对杠杆A端施加的举力分别为F1、人的重力和受力面积(与地的接触面积);
(2)再利用重力公式求人的质量;
(3)当滑轮下未挂重物时,他用力F1匀速举起杠杆的A端时所做的功为利用这个机械时的额外功,当滑轮下加挂重物G后,他用力F2匀速举起杠杆的A端所做的功为总功,根据机械效率的公式即可求整个滑轮组的机械效率η;
(4)根据滑轮下未挂重物时,动滑轮重力为100N,利用杠杆平衡求出力臂OA与OB的关系,再根据当加挂重物后他对杠杆A端施加的举力为F2,由杠杆平衡条件得出重物的重力,然后当将重物完全浸没在水中,根据重物受力情况求出对动滑轮的拉力G′,最后利用P=Fv即可求功率.
点评:本题考查压强的计算,注意分析出压强变化的原因,即可解答本题的杠杆A端的拉力和人的重力,正确理解在滑轮下未挂重物时,他用力匀速举起杠杆的A端所的功为整个机械的额外功,其实在杠杆、绳重和机械间摩擦忽略不计时,这个额外功就是对动滑轮所做的功,并在(4)问中结合动滑轮的重力,利用杠杆平衡条件得出杠杆的力臂关系,这是解答本题机械效率和绳端B的拉力F′的重要关键所在.本题难点太大.

练习册系列答案
相关题目
 (2010?平谷区二模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N.(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg)
(2010?平谷区二模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N.(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg) (2012?大兴区一模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向.(杠杆、绳重和机械间摩擦忽略不计)则当重物G被匀速提升过程中,滑轮组的机械效率为
(2012?大兴区一模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向.(杠杆、绳重和机械间摩擦忽略不计)则当重物G被匀速提升过程中,滑轮组的机械效率为