��Ŀ����
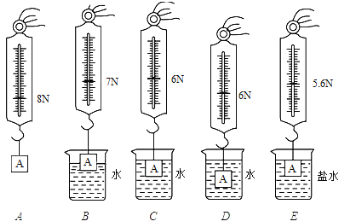
����Ŀ����ͼ��ʾ����һ�����ΪS=1000cm2 �� ��1.5m��Բ����ʢˮ��������ֱ����һ�����ΪS=200cm2 �� ��h=20cm��Բ������飺��֪�������ܶ�Ϊ��=2.5��103kg/m3 �� ������ˮ��H=1.2m����ʼʱ������±����������������С��϶��������ͼ��ʾ�Ĺ⻬�Ử��������������v=0.2m/s���ٶ�������������ȡg=10N/kg������ˮ����������ˮ=1.0��103kg/m3��

��1��������������ᱻ���ϣ�������������������У�����F����Сֵ�Ƕ��٣�
��2�������F���õ������ܳ��ܵ��������Ϊ40N����һ�������ܳ����㹻�������������ʱ������������ϣ�
���𰸡���1��30N����2��5.4s��
����������1���⣺������![]() �� ���������G����Vg��2.5��103kg/m3��200��10��4m2��0.2m��10N/kg��100N�� ��F������ҺgV���� �����ûʱ�ܵ��ĸ���F������ˮgV����1.0��103kg/m3��200��10��4m2��0.2m��10N/kg��40N�� ��ͼͨ�����������ӵĶ���n��2�� ��������������������У�����F����СֵΪ��F��
�� ���������G����Vg��2.5��103kg/m3��200��10��4m2��0.2m��10N/kg��100N�� ��F������ҺgV���� �����ûʱ�ܵ��ĸ���F������ˮgV����1.0��103kg/m3��200��10��4m2��0.2m��10N/kg��40N�� ��ͼͨ�����������ӵĶ���n��2�� ��������������������У�����F����СֵΪ��F��![]() ��G����F������
��G����F������![]() ��100N��40N����30N����������������ᱻ���ϣ�������������������У�����F����Сֵ��30N����2���⣺�������ǡ�ñ�����ʱ��F����
��100N��40N����30N����������������ᱻ���ϣ�������������������У�����F����Сֵ��30N����2���⣺�������ǡ�ñ�����ʱ��F����![]() ��G����F���䣩��F������G����2F����100N��2��40N��20N��V������
��G����F���䣩��F������G����2F����100N��2��40N��20N��V������![]() ��2��10��3m3 �� h����
��2��10��3m3 �� h����![]() ��0.1m������¶��ˮ����½�����V��S����h��V¶��V��V���䣬
��0.1m������¶��ˮ����½�����V��S����h��V¶��V��V���䣬
![]() ��2
��2![]() m��ʱˮ��H����H����h��1.2m��0.02m��1.18m���������������߶�h��H�䩁h����1.18m��0.1m��1.08m�����������Ͼ�����ʱ��t��
m��ʱˮ��H����H����h��1.2m��0.02m��1.18m���������������߶�h��H�䩁h����1.18m��0.1m��1.08m�����������Ͼ�����ʱ��t��![]() ��5.4s��
��5.4s��
�������F���õ������ܳ��ܵ��������Ϊ40N����5.4s���������ϣ�