题目内容
有两个铝块,它们的体积之比为3:2,当它们升高相同的温度,吸收的热量之比为 ;如果让它们放出相同的热量,那么它们降低的温度之比为 .
【答案】分析:知道两个铝块,得出两个铝块的密度、比热容相同,又知道体积关系,根据密度的公式变形m=ρV得出两个铝块的质量关系;
知道升高的温度相同,利用公式Q吸=cm△t求吸收的热量之比;知道放出相同的热量,利用放热公式的推导公式△t=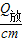 求降低的温度之比.
求降低的温度之比.
解答:解:由题知,两个都是铝块,
∴两个铝块的密度相同,比热容c相同,
∵m=ρV,v1:v2=3:2,ρ1=ρ2,
∴m1:m2=3:2,
两者升高的温度△t相同,
则它们吸收的热量之比为:
 =
= =
=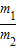 =
= ,
,
又∵Q放=cm△t,它们放出相同的热量,
∴ =
=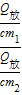 =
= ×
×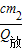 =
=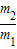 =
= .
.
故答案为:3:2,2:3.
点评:本题采用公式法求比值,就是将比式中的各比项用物理公式转换成它们的表达式,再相比求值的方法.
知道升高的温度相同,利用公式Q吸=cm△t求吸收的热量之比;知道放出相同的热量,利用放热公式的推导公式△t=
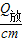 求降低的温度之比.
求降低的温度之比.解答:解:由题知,两个都是铝块,
∴两个铝块的密度相同,比热容c相同,
∵m=ρV,v1:v2=3:2,ρ1=ρ2,
∴m1:m2=3:2,
两者升高的温度△t相同,
则它们吸收的热量之比为:
 =
= =
=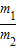 =
= ,
,又∵Q放=cm△t,它们放出相同的热量,
∴
 =
=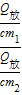 =
= ×
×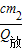 =
=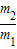 =
= .
. 故答案为:3:2,2:3.
点评:本题采用公式法求比值,就是将比式中的各比项用物理公式转换成它们的表达式,再相比求值的方法.

练习册系列答案
相关题目