Question

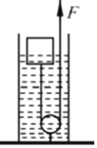
【题目】如图，水平桌面上放有一薄壁柱形容器，容器底面积为0.03m2，容器中装有水，质量为0.25kg、体积为1×10-3m3的正方体木块漂浮在水面上。现将细绳的一端绕过定滑轮后固定在木块下表面，并用竖直向上的拉力F缓慢匀速拉动细绳另一端，使木块从漂浮状态逐渐浸没入水中，木块不接触滑轮。不计摩擦与水的阻力，忽略绳重与体积的影响，g取10N/kg。求：

（1）木块漂浮时受到的浮力；

（2）若水深为0.3m，则容器底受到的水的压强；

（3）拉力F的最大值；

（4）木块从漂浮到被细绳拉到完全浸没，容器底部受到水的压强的变化量。

Answer 1

【答案】（1）2.5N（2）3×103Pa（3）7.5N（4）250Pa

【解析】

（1）木块漂浮时受到的浮力等于木块重力，利用F浮=G=mg计算；
（2）知道水深，利用p=ρgh求容器底受到的水的压强；
（3）当木块浸没时拉力F最大，此时木块排开水的体积等于木块的体积，利用阿基米德原理求木块受到的浮力；根据力的平衡可得：F浮=G木+F最大，据此求最大拉力；
（3）木块从漂浮到被细绳拉到完全浸没，水对容器底压力的变化量等于木块排开水的重力变化，即木块受到的浮力变化，再利用

求容器底部受到水的压强的变化量。

（1）木块漂浮时受到的浮力：

F浮=G木=m木g=0.25kg×10N/kg=2.5N；

（2）容器底受到的水的压强：

p=ρgh=1×103kg/m3×10N/kg×0.3m=3×103Pa；

（3）当木块浸没时所需拉力F最大，此时木块排开水的体积：

V排=V=1×10-3m3，

此时木块受到的浮力：

F浮′=ρ水gV排=1×103kg/m3×10N/kg×1×10-3m3=10N，

根据力的平衡条件可得：F浮′=G木+F最大，

所以最大拉力：

F最大=F浮′-G木=10N-2.5N=7.5N；

（3）木块从漂浮到被细绳拉到完全浸没，

水对容器底压力的变化量等于木块排开水的重力变化量，即木块受到的浮力变化量：

△F=△F浮=10N-2.5N=7.5N，

容器底部受到水的压强的变化量：

△p===250Pa。