题目内容
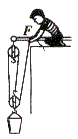
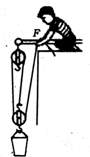 小明用如图所示的滑轮组将总重为180N的重物匀速提升3m,此时他测得这个滑轮组的机械效率为75%.不计绳重和滑轮的摩擦阻力,求:
小明用如图所示的滑轮组将总重为180N的重物匀速提升3m,此时他测得这个滑轮组的机械效率为75%.不计绳重和滑轮的摩擦阻力,求:(1)小明使用这个滑轮组提升重物的过程中,所做的有用功、额外功各是多少?
(2)若小明组装滑轮组所用的绳能承受的最大拉力为100N,则这个滑轮组能达到的最大机械效率是多少?
分析:(1)已知物重和提升的高度,利用公式W有用=Gh计算有用功;
已知有用功和机械效率,利用W总=
计算总功;已知总功和有用功,两者之差就是额外功;
(2)已知额外功和物体上升的高度,利用G0=
得到动滑轮重;已知承担物重的滑轮组绳子股数和绳子能承受的最大拉力,可以得到最大物重和动滑轮重之和,两者之差就是滑轮组提起的最大物重;已知最大物重和最大拉力,利用公式η=
计算最大机械效率.
已知有用功和机械效率,利用W总=
| W有用 |
| η |
(2)已知额外功和物体上升的高度,利用G0=
| W额 |
| h |
| G |
| nF |
解答:解:
(1)滑轮组做的有用功为W有用=Gh=180N×3m=540J
拉力做的总功为W总=
=
=720J
拉力做的额外功为W额=W总-W有用=720J-540J=180J
(2)动滑轮重为G0=
=
=60N
绳子能克服的最大总重为G总=3×100N=300N
最大物重为G最大=G总-G0=300N-60N=240N
滑轮组的最大机械效率为η最大=
=
=80%.
答:
(1)滑轮组做的有用功为540J;
拉力做的额外功为180J;
(2)滑轮组能达到的最大机械效率是80%.
(1)滑轮组做的有用功为W有用=Gh=180N×3m=540J
拉力做的总功为W总=
| W有用 |
| η |
| 540J |
| 75% |
拉力做的额外功为W额=W总-W有用=720J-540J=180J
(2)动滑轮重为G0=
| W额 |
| h |
| 180J |
| 3m |
绳子能克服的最大总重为G总=3×100N=300N
最大物重为G最大=G总-G0=300N-60N=240N
滑轮组的最大机械效率为η最大=
| G最大 |
| nF最大 |
| 240N |
| 3×100N |
答:
(1)滑轮组做的有用功为540J;
拉力做的额外功为180J;
(2)滑轮组能达到的最大机械效率是80%.
点评:利用滑轮组提升重物时应该清楚:在机械重一定,机械能够承受的范围之内,提升的物重越大,机械效率越高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
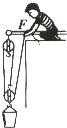 小明用如图所示的滑轮装置将总重为90N的重物匀速提升3m,此时他测得这个滑轮组的机械效率为75%.不计绳重和滑轮的摩擦阻力.
小明用如图所示的滑轮装置将总重为90N的重物匀速提升3m,此时他测得这个滑轮组的机械效率为75%.不计绳重和滑轮的摩擦阻力. (2009?鼓楼区一模)小明用如图所示的滑轮组,在4s内将质量为60kg的物体A匀速提升了0.5m.已知绳子自由端所用的拉力F为200N.这个过程中拉力的功率为多大?每个滑轮多重?(g取10N/kg,大小滑轮重一样)
(2009?鼓楼区一模)小明用如图所示的滑轮组,在4s内将质量为60kg的物体A匀速提升了0.5m.已知绳子自由端所用的拉力F为200N.这个过程中拉力的功率为多大?每个滑轮多重?(g取10N/kg,大小滑轮重一样) 小明用如图所示的滑轮组将一个重为120N的物体匀速提升2m,所用的拉力为50N,此时拉力所做的功为W,滑轮组的机械效率为η1;若仍用该滑轮纽提升一个重为170N的物体.此时滑轮组的机械效率为η2,则W、η1.η2分别是多少?(不计绳重和摩擦)
小明用如图所示的滑轮组将一个重为120N的物体匀速提升2m,所用的拉力为50N,此时拉力所做的功为W,滑轮组的机械效率为η1;若仍用该滑轮纽提升一个重为170N的物体.此时滑轮组的机械效率为η2,则W、η1.η2分别是多少?(不计绳重和摩擦)