题目内容
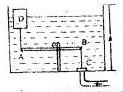
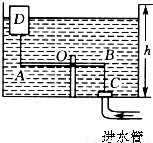
 如图为一水箱自动进水装置.其中杆AB能绕O点在竖直平面转动,OA=2OB,C处为进水管阀门,进水管口截面积为2厘米2,BC为一直杆,A点以一细绳与浮体D相连,浮体D是一个密度为0.4×103千克/米3的圆柱体,截面积为10厘米2,高为0.5米.细绳长为1米.若细绳、杆、阀的重不计,当AB杆水平时正好能堵住进水管,且O点距箱底1米.问;
如图为一水箱自动进水装置.其中杆AB能绕O点在竖直平面转动,OA=2OB,C处为进水管阀门,进水管口截面积为2厘米2,BC为一直杆,A点以一细绳与浮体D相连,浮体D是一个密度为0.4×103千克/米3的圆柱体,截面积为10厘米2,高为0.5米.细绳长为1米.若细绳、杆、阀的重不计,当AB杆水平时正好能堵住进水管,且O点距箱底1米.问;(1)若水箱高度h为3米,为防止水从水箱中溢出,进水管中水的压强不能超过多少;
(2)若进水管中水的压强为4.4×104帕,则水箱中水的深度为多少时,进水管停止进水.(取g=10牛/千克)
分析:(1)由题意可知,当水箱中的水恰好满时进水管中水的压强最大;分别对圆柱体、杠杆、进水管阀门受力分析,根据力的平衡条件和杠杆的平衡条件以及相互作用力的条件得出杠杆对进水管阀门的拉力;再根据F=Ps=ρgsh求出水箱中水对阀门的压力,进一步根据力的平衡条件求出进水管中水对阀门的压力,最后根据P=
求出进水管中水的最大压强.
(2)先根据F=Ps=ρgsh求出进水管中的水对阀门的压力,根据水深3米对进水口压力才为6N可知此时浮体起作用;根据阿基米德原理表示出此时浮体受到的浮力,根据力的平衡条件结合受力分析得出等式,解等式即可求出此时进水管停止进水时水箱中水的深度.
| F |
| s |
(2)先根据F=Ps=ρgsh求出进水管中的水对阀门的压力,根据水深3米对进水口压力才为6N可知此时浮体起作用;根据阿基米德原理表示出此时浮体受到的浮力,根据力的平衡条件结合受力分析得出等式,解等式即可求出此时进水管停止进水时水箱中水的深度.
解答:解:(1)如图受力分析:
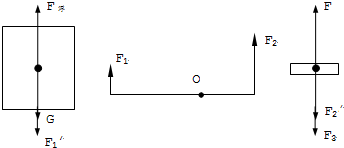
由第一幅图和第二幅图可得:F1=F1′=F浮-G=ρ水gs1h1-ρ柱gs1h1=(ρ水-ρ柱)gs1h1
=(1.0×103kg/m3-0.4×103kg/m3)×10N/kg×10×104m2×0.5m=3N,
由F1?0A=F2?OB可得:
F2′=F2=2F1=6N,
F3=P水S=ρ水gsh=1.0×103kg/m3×3m×2×10-4m2=6N,
由第三幅图可得:F=F2′+F3=6N+6N=12N,
进水管中水的压强不能超过P进=
=
=6.0×104Pa.
(2)F′=P进′S=4.4×104×2×10-4m2=8.8N,
由于水深3米对进水口压力才为6N,故浮体起作用时设水深为h′则
2ρ水gS1(h′-2m)-2ρ柱gS1h1+ρ水gh′S=F′,
整理可得:h′=
=
≈2.4m.
答:(1)进水管压强不超过6.0×104Pa;
(2)水箱中水的深度为2.4m.

由第一幅图和第二幅图可得:F1=F1′=F浮-G=ρ水gs1h1-ρ柱gs1h1=(ρ水-ρ柱)gs1h1
=(1.0×103kg/m3-0.4×103kg/m3)×10N/kg×10×104m2×0.5m=3N,
由F1?0A=F2?OB可得:
F2′=F2=2F1=6N,
F3=P水S=ρ水gsh=1.0×103kg/m3×3m×2×10-4m2=6N,
由第三幅图可得:F=F2′+F3=6N+6N=12N,
进水管中水的压强不能超过P进=
| F |
| S |
| 12N |
| 2×10-4m2 |
(2)F′=P进′S=4.4×104×2×10-4m2=8.8N,
由于水深3米对进水口压力才为6N,故浮体起作用时设水深为h′则
2ρ水gS1(h′-2m)-2ρ柱gS1h1+ρ水gh′S=F′,
整理可得:h′=
| F′+2(ρ水×2m+ρ柱h1)gS1 |
| (2S1+S)ρ水g |
=
| 8.8N +2 ×(1.0×103kg/m3×2m+0.4×103kg/m3×0.5m)×10N/kg×10×10-4m2 |
| (2×10×10-4m2+2×10-4m2)×1.0×103kg/m3×10N/kg |
≈2.4m.
答:(1)进水管压强不超过6.0×104Pa;
(2)水箱中水的深度为2.4m.
点评:此题综合性很强,且难度很大;解答时,从分析受力分析入手,再将题目进行分解:浮力问题、杠杆平衡条件问题、压强问题;将三类问题通过力有机的结合在一起,充分利用题目的已知条件,就可解答此题.

练习册系列答案
相关题目
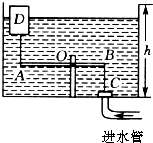 (2012?北京一模)如图为一水箱自动进水装置.其中水箱高h为3m,杆AB能绕O点在竖直平面转动,OA=2OB,且O点距箱底1m.C处为进水管阀门,阀门厚度不计,进水管口横截面积为2cm2.BC为一直杆,A点以一细绳与浮体D相连,浮体D是一个密度为0.4×103kg/m3的圆柱体,高为0.5m,细绳长为1m.细绳、杆、阀的重力不计,AB杆水平时正好能堵住进水管.当进水管中水的压强为P1时,水箱深度为2.4m.设进水管中水的最大压强为P2,且P1:P2=11:15.现在进水管中水的压强为P3,P3=3.3×104Pa,且P3<P1.求水箱中水的深度为多少时,进水管停止进水.(g取10N/kg)
(2012?北京一模)如图为一水箱自动进水装置.其中水箱高h为3m,杆AB能绕O点在竖直平面转动,OA=2OB,且O点距箱底1m.C处为进水管阀门,阀门厚度不计,进水管口横截面积为2cm2.BC为一直杆,A点以一细绳与浮体D相连,浮体D是一个密度为0.4×103kg/m3的圆柱体,高为0.5m,细绳长为1m.细绳、杆、阀的重力不计,AB杆水平时正好能堵住进水管.当进水管中水的压强为P1时,水箱深度为2.4m.设进水管中水的最大压强为P2,且P1:P2=11:15.现在进水管中水的压强为P3,P3=3.3×104Pa,且P3<P1.求水箱中水的深度为多少时,进水管停止进水.(g取10N/kg) 如图为一水箱自动进水装置.其中杆AB能绕O点在竖直平面转动,OA=2OB,C处为进水管阀门,进水管口截面积为2厘米2,BC为一直杆,A点以一细绳与浮体D相连,浮体D是一个密度为0.4×103千克/米3的圆柱体,截面积为10厘米2,高为0.5米.细绳长为1米.若细绳、杆、阀的重不计,当AB杆水平时正好能堵住进水管,且O点距箱底1米.问;
如图为一水箱自动进水装置.其中杆AB能绕O点在竖直平面转动,OA=2OB,C处为进水管阀门,进水管口截面积为2厘米2,BC为一直杆,A点以一细绳与浮体D相连,浮体D是一个密度为0.4×103千克/米3的圆柱体,截面积为10厘米2,高为0.5米.细绳长为1米.若细绳、杆、阀的重不计,当AB杆水平时正好能堵住进水管,且O点距箱底1米.问;