题目内容
 (2007?赤峰)如图是滑轮组提起重物装置的示意图,物体重G=6×104N滑轮组的机械效率为80%,拉力F的功率为2.5KW,要把重物匀速提升1m求:
(2007?赤峰)如图是滑轮组提起重物装置的示意图,物体重G=6×104N滑轮组的机械效率为80%,拉力F的功率为2.5KW,要把重物匀速提升1m求:(1)有用功和额外功分别是多少?
(2)需要的拉力F为多大?
(3)需要多长时间?
分析:(1)在已知物重和提升高度的情况下,利用公式W=Gh可直接计算有用功的大小;根据有用功与机械效率可得出总功的大小,有用功占80%,则额功外占20%,可求出额外功;
(2)求出总功的大小,再根据拉力移动的距离,可利用公式W=Fs的变形,求出拉力F的大小;
(3)知道功率,根据公式P=Fv的变形,可求出绳子自由端移动的速度,再根据提升的高度可得出提升的时间.
(2)求出总功的大小,再根据拉力移动的距离,可利用公式W=Fs的变形,求出拉力F的大小;
(3)知道功率,根据公式P=Fv的变形,可求出绳子自由端移动的速度,再根据提升的高度可得出提升的时间.
解答:解:(1)有用功:W有=Gh=6×104N×1m=6×104J
总功:W总=
=
=7.5×104J
额外功:W额=W总-W有=7.5×104J-6×104J=1.5×104J.
(2)读图可知,s=3h=3×1m=3m,
需要的拉力F=
=
=2.5×104N.
(3)绳端移动的速度:由公式P=Fv得,
v=
=
=0.1m/s
绳端需移动3m,则所需时间
t=
=
=30s.
答:(1)有用功为6×104J,额外功为1.5×104J;
(2)需要的拉力F为2.5×104N;
(3)需要的时间为30s.
总功:W总=
| W有 |
| η |
| 6×104J |
| 0.8 |
额外功:W额=W总-W有=7.5×104J-6×104J=1.5×104J.
(2)读图可知,s=3h=3×1m=3m,
需要的拉力F=
| W总 |
| s |
| 7.5×104J |
| 3m |
(3)绳端移动的速度:由公式P=Fv得,
v=
| P |
| F |
| 2.5×103W |
| 2.5×104N |
绳端需移动3m,则所需时间
t=
| s |
| v |
| 3m |
| 0.1m/s |
答:(1)有用功为6×104J,额外功为1.5×104J;
(2)需要的拉力F为2.5×104N;
(3)需要的时间为30s.
点评:本题主要考查了有用功、总功、额外功的求法,机械效率、功率、速度的计算等,虽然也用到的都是基本的常见公式,但考查的角度较为特殊,尤其最后的求提升物体的时间,有一定的新意,值得我们关注.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
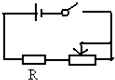 (2007?赤峰)如图所示,电阻R的阻值是30Ω,要求电阻R的电流能在10mA到100mA范围内连续可调,应该选用的电源电压最小值是
(2007?赤峰)如图所示,电阻R的阻值是30Ω,要求电阻R的电流能在10mA到100mA范围内连续可调,应该选用的电源电压最小值是