题目内容
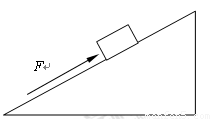
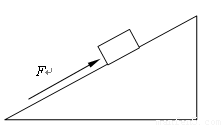
 如图所示,斜面长4m,高2m.质量为50kg的小明站在斜面顶端,用平行于斜面向上的75N的拉力将100N重的物体从斜面底端匀速拉到斜面顶端,g=10N/kg,求:
如图所示,斜面长4m,高2m.质量为50kg的小明站在斜面顶端,用平行于斜面向上的75N的拉力将100N重的物体从斜面底端匀速拉到斜面顶端,g=10N/kg,求:(1)小明对物体做的总功.
(2)斜面的机械效率.
(3)物体所受的摩擦阻力.
分析:(1)已知斜面的长和拉力F的大小,可以利用公式W=FS求出拉力F做的总功.
(2)知道物体的重力和提升的高度,可利用公式W=Gh计算出克服重力做的有用功;再利用公式η=
计算出斜面的机械效率.
(3)而有用功加上额外功(克服摩擦做功)等于总功,据此求出额外功,再利用公式W额外=fs求摩擦力大小.
(2)知道物体的重力和提升的高度,可利用公式W=Gh计算出克服重力做的有用功;再利用公式η=
| W有用 |
| W总 |
(3)而有用功加上额外功(克服摩擦做功)等于总功,据此求出额外功,再利用公式W额外=fs求摩擦力大小.
解答:解:
(1)∵s=4m,F=75N,
∴小明对物体做的总功为:W总=Fs=75N×4m=300J.
(2)∵G=100N,h=2m,
∴克服重力做的有用功为:W有用=Gh=100N×2m=200J,
则斜面的机械效率为:η=
=
≈66.7%.
(3)∵W总=300J,W有用=200J,
∴克服摩擦所做的额外功为:W额外=W总-W有用=300J-200J=100J,
而s=4m,
物体所受的摩擦阻力为:f=
=
=25N.
答:(1)小明对物体做的总功为300J.
(2)斜面的机械效率为66.7%.
(3)物体所受的摩擦阻力为25N.
(1)∵s=4m,F=75N,
∴小明对物体做的总功为:W总=Fs=75N×4m=300J.
(2)∵G=100N,h=2m,
∴克服重力做的有用功为:W有用=Gh=100N×2m=200J,
则斜面的机械效率为:η=
| W有用 |
| W总 |
| 200J |
| 300J |
(3)∵W总=300J,W有用=200J,
∴克服摩擦所做的额外功为:W额外=W总-W有用=300J-200J=100J,
而s=4m,
物体所受的摩擦阻力为:f=
| W额外 |
| s |
| 100J |
| 4m |
答:(1)小明对物体做的总功为300J.
(2)斜面的机械效率为66.7%.
(3)物体所受的摩擦阻力为25N.
点评:本题考查有用功、总功、额外功和机械效率的计算,关键是公式和公式变形的应用,知道额外功等于克服摩擦阻力做的功,解题的关键在于明确总功应等于有用功与额外功之和.,注意f≠F,这是本题的易错点.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
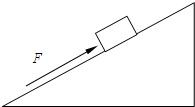 如图所示,斜面长4m,高2m,工人用400N的力沿斜面将重为600N的箱子,从底端推到顶端.下列说法中正确的是( )
如图所示,斜面长4m,高2m,工人用400N的力沿斜面将重为600N的箱子,从底端推到顶端.下列说法中正确的是( )| A、有用功为1800J,总功1200J | B、有用功为1200J,额外功为800J | C、总功为1600J,机械效率为75% | D、总功为800J,机械效率为75% |
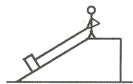 (2010?荆州)如图所示,斜面长4m,高2m.质量为50kg的小明站在斜面顶端,用平行于斜面向上的75N的拉力将100N重的物体从斜面底端匀速拉到斜面顶端,g=10N/kg,那么 ( )
(2010?荆州)如图所示,斜面长4m,高2m.质量为50kg的小明站在斜面顶端,用平行于斜面向上的75N的拉力将100N重的物体从斜面底端匀速拉到斜面顶端,g=10N/kg,那么 ( )