题目内容
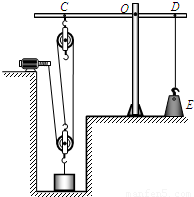
 如图所示是某科技小组设计的一个提升重物的装置,CD是一个以O点为转轴的水平杠杆,CO:OD=3:2.滑轮组固定在杠杆C点,通过固定在水平地面的电动机匀速提升重物,每个滑轮的质量均为m0.放置在水平地面上的配重E通过细绳竖直拉着杠杆D点,使杠杆CD始终保持水平平衡,配重E的质量mE为100kg.当电动机用拉力F1匀速提升重物A时,滑轮组的机械效率为η1,物体A匀速上升的速度为v1;当电动机用拉力F2匀速提升重物B时,滑轮组的机械效率为η2,物体B匀速上升的速度为v2.在匀速提升重物A、B的过程中,电动机的功率保持不变.已知F2-F1=50N,v1:v2=5:4,η2=90%.细绳和杠杆的质量、滑轮与轴的摩擦均忽略不计,g取10N/kg.求:
如图所示是某科技小组设计的一个提升重物的装置,CD是一个以O点为转轴的水平杠杆,CO:OD=3:2.滑轮组固定在杠杆C点,通过固定在水平地面的电动机匀速提升重物,每个滑轮的质量均为m0.放置在水平地面上的配重E通过细绳竖直拉着杠杆D点,使杠杆CD始终保持水平平衡,配重E的质量mE为100kg.当电动机用拉力F1匀速提升重物A时,滑轮组的机械效率为η1,物体A匀速上升的速度为v1;当电动机用拉力F2匀速提升重物B时,滑轮组的机械效率为η2,物体B匀速上升的速度为v2.在匀速提升重物A、B的过程中,电动机的功率保持不变.已知F2-F1=50N,v1:v2=5:4,η2=90%.细绳和杠杆的质量、滑轮与轴的摩擦均忽略不计,g取10N/kg.求:
(1)拉力F1的大小;
(2)滑轮组的机械效率η1;
(3)当电动机用拉力F2匀速提升重物B时,配重E对地面的压力N2.
解:(1)因为在匀速提升重物A、B的过程中,电动机的功率保持不变,因为P=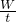 =
=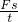 =Fv,所以:
=Fv,所以:
P=F1×3v1=F2×3v2,解得:F1:F2=v2:v1=4:5,
又因为F2-F1=50N,所以F1=200N,F2=250N;
(2)以动滑轮和重物A整体为研究对象,进行受力分析,如图所示.
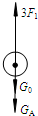
3F1=G0+GA …①
同理有3F2=G0+GB …②
当电动机用拉力F2匀速提升重物B时,滑轮组的机械效率为η2=90%,
η2= ×100%=
×100%= ×100%=
×100%=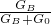 ×100%=
×100%= ,
,
GB:G动=9:1,③
由①②③联立得:GA=525N,GB=675N,G0=75N.
当电动机用拉力F1匀速提升重物A时,滑轮组的机械效率为η1,
η1= ×100%=
×100%= ×100%=
×100%=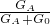 ×100%=
×100%=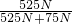 ×100%=87.5%;
×100%=87.5%;
(3)当电动机用拉力F2匀速提升重物B时,设滑轮组对杠杆C点的拉力为FC2,配重E对杠杆D点的拉力为FD2,地面对配重E的支持力为N2.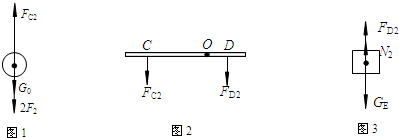
以定滑轮为研究对象,进行受力分析,如图1所示,
FC2=G0+2 F2=75N+2×250N=575N,
以杠杆CD为研究对象进行受力分析,如图2所示,
FC2×OC=FD2×OD,
解得:FD2=FC2× =575N×
=575N× =862.5N,
=862.5N,
以配重E为研究对象,进行受力分析,如图3所示.
FD2+N2=GE
得:配重E对地面的压力:N2=GE-FD2=mEg-FD2=100kg×10N/kg-862.5N=137.5N.
答:(1)拉力F1的大小为200N;
(2)滑轮组的机械效率η1为87.5%;
(3)配重E对地面的压力为137.5N.
分析:(1)匀速提升重物A、B的过程中,电动机的功率保持不变,根据P=Fv和v2:v1=4:5求出拉力F的大小;
(2)首先根据题意求出物体A和B的重力、动滑轮的重力,再根据公式η= =
= =
= 求出滑轮组的机械效率;
求出滑轮组的机械效率;
(3)根据杠杆的平衡条件求出对配重E的拉力,再根据二力平衡条件求出配重E对地面的压力.
点评:此类问题是一道复杂的综合题目,要会正确的对物体进行受力分析,结合平衡状态求解出各力的大小,进而利用杠杆的平衡条件和机械效率计算公式进行分析求解.
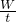 =
=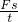 =Fv,所以:
=Fv,所以:P=F1×3v1=F2×3v2,解得:F1:F2=v2:v1=4:5,
又因为F2-F1=50N,所以F1=200N,F2=250N;
(2)以动滑轮和重物A整体为研究对象,进行受力分析,如图所示.

3F1=G0+GA …①
同理有3F2=G0+GB …②
当电动机用拉力F2匀速提升重物B时,滑轮组的机械效率为η2=90%,
η2=
 ×100%=
×100%= ×100%=
×100%=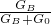 ×100%=
×100%= ,
,GB:G动=9:1,③
由①②③联立得:GA=525N,GB=675N,G0=75N.
当电动机用拉力F1匀速提升重物A时,滑轮组的机械效率为η1,
η1=
 ×100%=
×100%= ×100%=
×100%=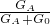 ×100%=
×100%=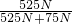 ×100%=87.5%;
×100%=87.5%; (3)当电动机用拉力F2匀速提升重物B时,设滑轮组对杠杆C点的拉力为FC2,配重E对杠杆D点的拉力为FD2,地面对配重E的支持力为N2.

以定滑轮为研究对象,进行受力分析,如图1所示,
FC2=G0+2 F2=75N+2×250N=575N,
以杠杆CD为研究对象进行受力分析,如图2所示,
FC2×OC=FD2×OD,
解得:FD2=FC2×
 =575N×
=575N× =862.5N,
=862.5N,以配重E为研究对象,进行受力分析,如图3所示.
FD2+N2=GE
得:配重E对地面的压力:N2=GE-FD2=mEg-FD2=100kg×10N/kg-862.5N=137.5N.
答:(1)拉力F1的大小为200N;
(2)滑轮组的机械效率η1为87.5%;
(3)配重E对地面的压力为137.5N.
分析:(1)匀速提升重物A、B的过程中,电动机的功率保持不变,根据P=Fv和v2:v1=4:5求出拉力F的大小;
(2)首先根据题意求出物体A和B的重力、动滑轮的重力,再根据公式η=
 =
= =
= 求出滑轮组的机械效率;
求出滑轮组的机械效率;(3)根据杠杆的平衡条件求出对配重E的拉力,再根据二力平衡条件求出配重E对地面的压力.
点评:此类问题是一道复杂的综合题目,要会正确的对物体进行受力分析,结合平衡状态求解出各力的大小,进而利用杠杆的平衡条件和机械效率计算公式进行分析求解.

练习册系列答案
相关题目
 如图所示是某科技小组设计的一个提升重物的装置,CD是一个以O点为转轴的水平杠杆,CO:OD=3:2.滑轮组固定在杠杆C点,通过固定在水平地面的电动机匀速提升重物,每个滑轮的质量均为m0.放置在水平地面上的配重E通过细绳竖直拉着杠杆D点,使杠杆CD始终保持水平平衡,配重E的质量mE为100kg.当电动机用拉力F1匀速提升重物A时,滑轮组的机械效率为η1,物体A匀速上升的速度为v1;当电动机用拉力F2匀速提升重物B时,滑轮组的机械效率为η2,物体B匀速上升的速度为v2.在匀速提升重物A、B的过程中,电动机的功率保持不变.已知F2-F1=50N,v1:v2=5:4,η2=90%.细绳和杠杆的质量、滑轮与轴的摩擦均忽略不计,g取10N/kg.求:
如图所示是某科技小组设计的一个提升重物的装置,CD是一个以O点为转轴的水平杠杆,CO:OD=3:2.滑轮组固定在杠杆C点,通过固定在水平地面的电动机匀速提升重物,每个滑轮的质量均为m0.放置在水平地面上的配重E通过细绳竖直拉着杠杆D点,使杠杆CD始终保持水平平衡,配重E的质量mE为100kg.当电动机用拉力F1匀速提升重物A时,滑轮组的机械效率为η1,物体A匀速上升的速度为v1;当电动机用拉力F2匀速提升重物B时,滑轮组的机械效率为η2,物体B匀速上升的速度为v2.在匀速提升重物A、B的过程中,电动机的功率保持不变.已知F2-F1=50N,v1:v2=5:4,η2=90%.细绳和杠杆的质量、滑轮与轴的摩擦均忽略不计,g取10N/kg.求: