��Ŀ����
����ͬѧһֻЬ�������S������˫��վ��ˮƽ�����Ͼ�ֹʱ�Ե����ѹǿΪp1����������ͼ1��ʾ�Ļ�����������������A��ʹ����A��ˮƽ��������v1�ٶ���ֱ���ƶ�tʱ�䣬��ʱ���Ե����ѹǿΪp2���˺������ô˻�����������������A��ʹ����ˮƽ��������v2�ٶȣ�v2��v1����ֱ���ƶ���ͬʱ�䣻��ʱ������Ļ�еЧ��Ϊ��1��������ǰ�������������������ɶ˵�������С���䣮���������غͻ��ִ���Ħ���������������У�����1ʼ����ˮƽ������������ʼ������ֱ������������������ݣ�
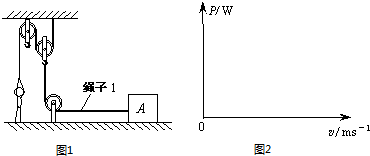
��1�����˶��������ɶ˵������Ƕ��٣�
��2��������A�ܵ���Ħ�����Ƕ��٣�
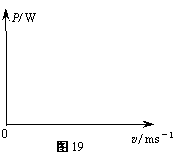
��3����ͼ2�У������Ļ����������ɶ������Ĺ���P�������ƶ��ٶ�v�仯��ͼ��
��4����������A�ϱ����ٷ�һ����B��ͼ��δ��������ʹ����A��Bһ����ˮƽ����������ֱ���˶�����ʱ��װ�õĻ�еЧ��Ϊ��2��������A�ܵ���Ħ�����Ƕ��٣�

��1�����˶��������ɶ˵������Ƕ��٣�
��2��������A�ܵ���Ħ�����Ƕ��٣�
��3����ͼ2�У������Ļ����������ɶ������Ĺ���P�������ƶ��ٶ�v�仯��ͼ��
��4����������A�ϱ����ٷ�һ����B��ͼ��δ��������ʹ����A��Bһ����ˮƽ����������ֱ���˶�����ʱ��װ�õĻ�еЧ��Ϊ��2��������A�ܵ���Ħ�����Ƕ��٣�
��������1������˶Ե����ѹǿ�仯��������p=
���ѹ���仯�����˶����ӵ����������˶Ե����ѹ���仯����
��2�������������п˷�Ħ�������Ĺ�Ϊ���ù������ݦ�=
=
=
���Ħ������С��
��3�������ƶ��ٶ�v=2v��������P=
=
=Fv��֪����������ʱ�������Ĺ��������ٶȳ����ȣ���������ͼ��
��4���������غͻ��ִ���Ħ��������F=
��f+G��������������أ��ٸ��ݦ�=
=
=
���Ħ������
| F |
| S |
��2�������������п˷�Ħ�������Ĺ�Ϊ���ù������ݦ�=
| W���� |
| W�� |
| fs�� |
| F2s�� |
| f |
| 2F |
��3�������ƶ��ٶ�v=2v��������P=
| W |
| t |
| Fs |
| t |
��4���������غͻ��ִ���Ħ��������F=
| 1 |
| 2 |
| W���� |
| W�� |
| f��s�� |
| f��s��+G��s�� |
| f�� |
| f��+G�� |
����⣺��1���˶Ե����ѹǿ�仯����p=p1-p2��
��p=
���˶����ӵ�������
F=��F=��p2S=2��p1-p2��S��
��2���ߦ�1=
=
=
=
��Ħ����f=4S��p1-p2����1��
��3�������ƶ��ٶ�v=2v�������������Ĺ���P=
=
=Fv=2Fv��=4S��p1-p2��v������������ʱ�������Ĺ��������ٶȳ����ȣ�ͼ�����£�

��4���������غͻ��ִ���Ħ����
��F=
��f+G����
�ද������G��=2F-f=2��2��p1-p2��S-4S��p1-p2����1=4S��p1-p2����1-��1����
�ߦ�2=
=
=
��Ħ����f��=
=
��
�𣺣�1���˶��������ɶ˵�������2��p1-p2��S��
��2������A�ܵ���Ħ������4S��p1-p2����1��
��3��ͼ�����ͼ��
��4������A�ܵ���Ħ������
��
��p=
| F |
| S |
���˶����ӵ�������
F=��F=��p2S=2��p1-p2��S��
��2���ߦ�1=
| W���� |
| W�� |
| fs�� |
| F2s�� |
| f |
| 2F |
| f |
| 2��2(p1-p2)S |
��Ħ����f=4S��p1-p2����1��
��3�������ƶ��ٶ�v=2v�������������Ĺ���P=
| W |
| t |
| Fs |
| t |

��4���������غͻ��ִ���Ħ����
��F=
| 1 |
| 2 |
�ද������G��=2F-f=2��2��p1-p2��S-4S��p1-p2����1=4S��p1-p2����1-��1����
�ߦ�2=
| W���� |
| W�� |
| f��s�� |
| f��s��+G��s�� |
| f�� |
| f��+G�� |
��Ħ����f��=
| G����2 |
| 1-��2 |
| 4S(p1-p2)(1-��1)��2 |
| 1-��2 |
�𣺣�1���˶��������ɶ˵�������2��p1-p2��S��
��2������A�ܵ���Ħ������4S��p1-p2����1��
��3��ͼ�����ͼ��
��4������A�ܵ���Ħ������
| 4S(p1-p2)(1-��1)��2 |
| 1-��2 |
������������һ����ѧ�ۺ��⣬��ѹǿ��ѹ�����㡢���ù����ܹ�����еЧ�ʼ���ͻ�����ʡ������ļ���ȣ��ѶȺܴ�

��ϰ��ϵ�д�
 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
�����Ŀ
 ��2012?̫����ģ�⣩���������ؼƺͷ���ֽ������վ��ʱ�Ե����ѹǿ��ʵ���У�����˵�����Ϊ54kg���ڷ���ֽ������Ь��Ьӡ����ͼ��ʾ����ÿһ����������Ϊ4��10-4m2��������ʱ������������һ������ĺ��Բ��ƣ���һֻЬ�������
��2012?̫����ģ�⣩���������ؼƺͷ���ֽ������վ��ʱ�Ե����ѹǿ��ʵ���У�����˵�����Ϊ54kg���ڷ���ֽ������Ь��Ьӡ����ͼ��ʾ����ÿһ����������Ϊ4��10-4m2��������ʱ������������һ������ĺ��Բ��ƣ���һֻЬ�������