题目内容
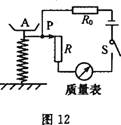
某电子天平原理图如图所示，A为托盘，R 为滑动变阻器，滑片P通过一个连杆固定在弹簧上．当托盘中放上物体时，滑片向下滑动到某位置，从质量表上可读出所放物体的质量．当托盘中不放物体时，滑片在R的最上端．已知R0=5Ω，R的最大阻值为25Ω，电源电压为3V且保持不变，图中的质量表相当于电流表．试求：
（1）当所测质量达到最大值时，电路中的电流是多少？
（2）不测质量时，通电5min，滑动变阻器R消耗的电能是多少？
解：（1）测最大质量时，滑片P在R的最下端，电路为R0的简单电路，
根据欧姆定律可得，电路中的电流：
I=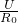
=
=0.6A；
（2）不测质量时，滑片P在R的最上端，R与R0串联，
∵串联电路中总电阻等于各分电阻之和，
∴电路中的电流：
I串=
=
=0.1A，
变阻器消耗电能：
W=I串2Rt=（0.1A）2×25Ω×5×60s=75J．
答：（1）当所测质量达到最大值时，电路中的电流是0.6A．
（2）不测质量时，通电5min，滑动变阻器R消耗的电能是75J．
分析：（1）测最大质量时，滑片P在R的最下端，电路为R0的简单电路，根据欧姆定律求出电路中的电流；
（2）不测质量时，R0与滑动变阻器的最大阻值串联，根据电阻的串联和欧姆定律求出电路中的电流，再根据W=UIt=I2Rt求出滑动变阻器R消耗的电能．
点评：本题考查了串联电路的特点和欧姆定律、电功率公式的应用，关键是知道质量达到最大和不测量时电路的连接情况．
根据欧姆定律可得，电路中的电流：
I=
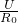==0.6A；（2）不测质量时，滑片P在R的最上端，R与R0串联，
∵串联电路中总电阻等于各分电阻之和，
∴电路中的电流：
I串=
==0.1A，变阻器消耗电能：
W=I串2Rt=（0.1A）2×25Ω×5×60s=75J．
答：（1）当所测质量达到最大值时，电路中的电流是0.6A．
（2）不测质量时，通电5min，滑动变阻器R消耗的电能是75J．
分析：（1）测最大质量时，滑片P在R的最下端，电路为R0的简单电路，根据欧姆定律求出电路中的电流；
（2）不测质量时，R0与滑动变阻器的最大阻值串联，根据电阻的串联和欧姆定律求出电路中的电流，再根据W=UIt=I2Rt求出滑动变阻器R消耗的电能．
点评：本题考查了串联电路的特点和欧姆定律、电功率公式的应用，关键是知道质量达到最大和不测量时电路的连接情况．
练习册系列答案
备战中考寒假系列答案
相关题目
（2012?和平区模拟）某物理探究小组学习关于比热容的知识后，结合生活经验，提出了疑问：质量相同的不同液体沸腾变为气体时吸收的热量是否相同呢？
（2013?大连二模）某电子天平原理图如图所示，A为托盘，R 为滑动变阻器，滑片P通过一个连杆固定在弹簧上．当托盘中放上物体时，滑片向下滑动到某位置，从质量表上可读出所放物体的质量．当托盘中不放物体时，滑片在R的最上端．已知R0=5Ω，R的最大阻值为25Ω，电源电压为3V且保持不变，图中的质量表相当于电流表．试求：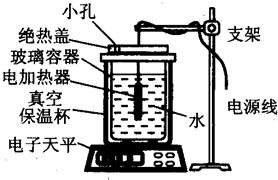
单位质量的某种液体变为同温度的气体所需要吸收的热量，叫做这种液体的汽化热．通常情况下，同种液体在不同温度下的汽化热是不同的．某课外活动小组设计了如图所示的装置，可以用来测定100℃时水的汽化热．该装置的测量原理是：用电压可调的电加热器使玻璃容器内的水沸腾，用电子天平分别测量沸腾一段时间前后水的质量，同时测量所用的时间及在该段时间内电加热器的电压和电流，根据相关的数据和能量守恒关系即可求出水的汽化热λ．由于这个装置工作时的散热损失是不可忽略的，该组同学实验时测量了两组数据，如下表所示：