题目内容
一位工人用滑轮组将重1500N的货物提升到高2m的仓库货架上,他所用拉力为500N,绳子自由端被拉下了8m,则:(1)请你根据题中要求,直接在图上画出工人提升重物时的滑轮组的绕法;
(2)提升货物时,工人做的总功为多少?
(3)提升货物所花时间为1min,则这位工人的功率为多少?
(4)此滑轮组的机械效率为多少?

【答案】分析:(1)知道物体上升的高度和拉力端移动的距离,利用s=nh求承担物重的绳子股数,进而确定滑轮组的绕法;
(2)已知拉力的大小和拉力移动的距离,根据公式W=Fs可求拉力做的总功;
(3)知道做功的时间,根据公式P=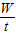 可求这位工人的功率;
可求这位工人的功率;
(4)由图知承担物重的绳子股数n=4,利用s=4h求物体上升的高度h,根据公式W=Gh可求克服物体重力做的有用功,有用功与总功的比值就是滑轮组的机械效率.
解答:解:
(1)由题知,h=2m,s=8m,由s=nh可得承担物重的绳子股数:n=4,即由4段绳子承担物重,如图所示:
(2)拉力做的功:
W=Fs=500N×8m=4000J;
(3)这位工人的功率:
P= =
=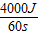 ≈66.7W;
≈66.7W;
(4)物体上升的高度h=2m
拉力做的有用功W有用=Gh=1500N×2m=3000J
滑轮组的机械效率:
η= ×100%=
×100%= ×100%=75%.
×100%=75%.
答:(1)如图所示;
(2)提升货物时,工人做的总功为4000J
(3)提升货物所花时间为1min,则这位工人的功率为66.7W;
(4)此滑轮组的机械效率为75%.
点评:本题考查使用滑轮组功、功率、机械效率的计算,关键是公式及其变形的灵活运用,根据物体升高的高度和拉力端移动的距离确定承担物重的绳子股数是本题的突破口.
(2)已知拉力的大小和拉力移动的距离,根据公式W=Fs可求拉力做的总功;
(3)知道做功的时间,根据公式P=
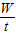 可求这位工人的功率;
可求这位工人的功率;(4)由图知承担物重的绳子股数n=4,利用s=4h求物体上升的高度h,根据公式W=Gh可求克服物体重力做的有用功,有用功与总功的比值就是滑轮组的机械效率.
解答:解:
(1)由题知,h=2m,s=8m,由s=nh可得承担物重的绳子股数:n=4,即由4段绳子承担物重,如图所示:

(2)拉力做的功:
W=Fs=500N×8m=4000J;
(3)这位工人的功率:
P=
 =
=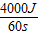 ≈66.7W;
≈66.7W;(4)物体上升的高度h=2m
拉力做的有用功W有用=Gh=1500N×2m=3000J
滑轮组的机械效率:
η=
 ×100%=
×100%= ×100%=75%.
×100%=75%.答:(1)如图所示;
(2)提升货物时,工人做的总功为4000J
(3)提升货物所花时间为1min,则这位工人的功率为66.7W;
(4)此滑轮组的机械效率为75%.
点评:本题考查使用滑轮组功、功率、机械效率的计算,关键是公式及其变形的灵活运用,根据物体升高的高度和拉力端移动的距离确定承担物重的绳子股数是本题的突破口.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

 一位工人用滑轮组将重1500N的货物匀速提升到高2m的仓库货架上,整个过程他所用拉力为500N,绳子自由端移动了8m,则:
一位工人用滑轮组将重1500N的货物匀速提升到高2m的仓库货架上,整个过程他所用拉力为500N,绳子自由端移动了8m,则:
