题目内容
（2013?太仓市模拟）如图所示，电源电压保持不变，闭合开关S．当滑动变阻器的滑片P位于某一位置时，电压表V1的示数是10V，电压表V2的示数是5V，滑动变阻器接入电路中的电阻与电阻R2的总电功率为5W；当滑动变阻器的滑片P位于最左端时，电压表V2的示数是2V，滑动变阻器接入电路中的电阻与电阻R2的总电功率为3.2W．求滑动变阻器的最大阻值．分析：先根据题意画出等效电路图，由甲图利用欧姆定律和串联电路的电流特点求出R1、R2之间的关系；再由甲、乙两图中R2两端的电压关系求出电流关系，由电功率关系结合P=I2R得出等式；再根据电源的电压不变列出等式，联立等式得出RA、RB与R2之间的关系，再由图甲中电流和电阻关系及已知功率求出R2的电功率，从而根据R=
求出R2的阻值，进一步求出滑动变阻器的最大阻值．
| U2 |
| P |
解答：解：开关S闭合，当滑动变阻器滑片P位于某一位置时，等效电路图如图甲所示．
开关S闭合，当滑动变阻器滑片P位于最左端时，等效电路图如图乙所示．
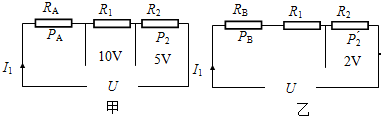
由图甲可得：10V=I1R1，5V=I2R2，
∴R1=2R2；
由图甲和图乙可得：5V=I1R2，2V=I2R2，
∴
=
；
5W=I12（RA+R2），3.2W=I22（RB+R2），
解得：4RA+3R2=RB-----------①
∵电源的电压不变，
∴U=I1（RA+R1+R2）=I2（RB+R1+R2）
解得：5RA+9R2=2RB------------②
由①②式解得RA=R2，RB=7R2，
由图甲可得：
=
，
即P2=2.5W，
由P=
得：R2=
=
=10Ω，
∴RB=7R2=7×10Ω=70Ω．
答：滑动变阻器的最大阻值为70Ω．
开关S闭合，当滑动变阻器滑片P位于最左端时，等效电路图如图乙所示．
由图甲可得：10V=I1R1，5V=I2R2，
∴R1=2R2；
由图甲和图乙可得：5V=I1R2，2V=I2R2，
∴
| I1 |
| I2 |
| 5 |
| 2 |
5W=I12（RA+R2），3.2W=I22（RB+R2），
解得：4RA+3R2=RB-----------①
∵电源的电压不变，
∴U=I1（RA+R1+R2）=I2（RB+R1+R2）
解得：5RA+9R2=2RB------------②
由①②式解得RA=R2，RB=7R2，
由图甲可得：
| 5W |
| P2 |
| RA+R2 |
| R2 |
即P2=2.5W，
由P=
| U2 |
| R |
| U22 |
| P2 |
| (5V)2 |
| 2.5W |
∴RB=7R2=7×10Ω=70Ω．
答：滑动变阻器的最大阻值为70Ω．
点评：本题是有关串联电路的特点和欧姆定律、电功率的综合计算题目．在解题过程中，注意电路的分析，根据已知条件分析出各种情况下的等效电路图，同时要注意在串联电路中各物理量之间的关系，结合题目中给出的已知条件进行解决．
练习册系列答案
相关题目