题目内容
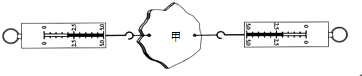
【题目】某小组同学研究柱形物体浸入液体的过程中液体对容器底部压力的变化情况,他们将高H为0.15米、横截面积为S的圆柱体挂在测力计下,并将其逐步浸入同一容器的液体中(液体不溢出),如图所示,记录其下表面到水面的距离h,计算出相邻两次实验中h的变化量△h,并测得容器底部受到液体的压力F液 , 将数据记录在表一中.然后,他们变换液体重复实验,将数据记录在表二中.(已知:ρ1>ρ2) ![]()
表一(液体密度为ρ1)
实验 | h | F液 | △h | △F液 |
1 | 0 | 20.0 | 0.01 | 1.0 |
2 | 0.01 | 21.0 | ||
3 | 0.02 | 22.0 | 0.02 | 2.0 |
4 | 0.04 | 24.0 | ||
5 | 0.05 | 25.0 | 0.03 | 3.0 |
6 | 0.08 | 28.0 | ||
7 | 0.15 | 35.0 | 0.01 | 0 |
8 | 0.16 | 35.0 |
表二(液体密度为ρ2)
实验 | h | F液 | △h | △F液 |
9 | 0 | 20.0 | 0.01 | 0.8 |
10 | 0.01 | 20.8 | ||
11 | 0.02 | 21.6 | 0.02 | 1.6 |
12 | 0.04 | 23.2 | ||
13 | 0.05 | 24.0 | 0.03 | 2.4 |
14 | 0.08 | 26.4 | ||
15 | 0.15 | 32.0 | 0.02 | 0 |
16 | 0.17 | 32.0 |
(1)分析比较实验序号1~6或9~14中△F液与△h的数据及相关条件,可得出的初步结论是: .
(2)分析比较实验序号1~6和9~14中△F液与△h的数据及相关条件,可得出的初步结论是: .
(3)分析比较实验序号7、8或15、16中的数据及相关条件,发现数据与上述的结论不相符合,简述数据与小红结论不符的原因 .
(4)请进一步综合分析表一、表二的相关数据,并归纳得出结论.
该小组同学认为物体浸入液体的过程中容器底部受到液体压力的增加量△F液除了与h和液体种类有关之外,可能还与物体自身的形状有关,为了验证自己的想法,需添加的器材为 .
器材:
圆柱体甲 高 H=0.15米 横截面积 2S;
正方体乙 边长H=0.15米 横截面积 S;
圆柱体丙 高 H=0.2米 横截面积 S.
【答案】
(1)在圆柱体没有全部浸没液体中之前,圆柱体浸入同种液体的过程中,△F液与△h的比值是一个定值
(2)在圆柱体没有全部浸没液体中之前,在圆柱体浸入不同种液体过程中,△F液与△h的比值是不同的,液体密度越大,比值越大
(3)圆柱体完全浸没,在液体中的深度增加,但液体的深度不再发生变化
(4)正方体乙
【解析】解:(1)分析比较实验序号1~6或9~14等数据中△F液与△h的关系及相关条件,容器底受到的液体压力的变化与深度的变化比值不变,为一定值,可得出的初步结论是:在圆柱体没有全部浸没液体中之前,圆柱体浸入同种液体的过程中,△F液与△h的比值是一个定值;(2)分析比较实验序号1~6和9~14中△F液与△h的数据及相关条件,同样计算△F液与△h的比值进行比较,可得到初步结论:在圆柱体没有全部浸没液体中之前,在圆柱体浸入不同种液体过程中,△F液与△h的比值是不同的,液体密度越大,比值越大.(3)分析实验序号7、8或15、16中的数据及相关条件,发现圆柱体浸入液体中的深度h大于圆柱体的高度0.15m时,随着深度的增加,圆柱体排开液体的体积不再变化,液体的深度也不再变化,所以压力F液不再随h而变化.(4)根据以上分析,要探究压力变化与物体形状的关系,要保持其它量相同,所以圆柱体的横截面积和高度不能发生变化,只有形状发生变化,因此要选择正方体乙.
所以答案是:(1)在圆柱体没有全部浸没液体中之前,圆柱体浸入同种液体的过程中,△F液与△h的比值是一个定值;(2)在圆柱体没有全部浸没液体中之前,在圆柱体浸入不同种液体过程中,△F液与△h的比值是不同的,液体密度越大,比值越大;(3)圆柱体完全浸没,在液体中的深度增加,但液体的深度不再发生变化;(4)正方体乙.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案