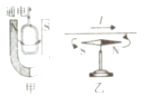
题目内容
【题目】如图所示,完全相同的圆柱形容器中,装有不同的两种液体甲、乙,在两容器中,距离同一高度分别有A、B两点.若两种液体的质量相等,则A、B两点的压强关系是pApB;若A、B两点的压强相等,则两种液体对容器底的压强关系是p甲p乙(两空选填“>”、“=”或“<”).
【答案】<;>
【解析】解:由于两种液体的质量相等时,甲液体的体积小于乙液体的体积,根据ρ=![]() 知甲液体的密度大于乙液体的密度,由于A、B两点离容器底等高,故A点距容器底这段液体产生的压强较大;但又由于二种液体的质量相等,所以它们对容器底的压力是相等的,面积又相等,故两种液体对容器底的压强相等;故A点的压强pA等于液体对容器底的压强减去A点距容器底的那段液体产生的压强,故pA<pB;
知甲液体的密度大于乙液体的密度,由于A、B两点离容器底等高,故A点距容器底这段液体产生的压强较大;但又由于二种液体的质量相等,所以它们对容器底的压力是相等的,面积又相等,故两种液体对容器底的压强相等;故A点的压强pA等于液体对容器底的压强减去A点距容器底的那段液体产生的压强,故pA<pB;
若A、B两点的压强相等,但A点距液面的高度比B点小,由公式p=ρgh可知,甲液体的密度大于乙液体的密度,又因为A、B两点离容器底等高,故A点距容器底这段液体产生的压强较大,则两种液体对容器底的压强应该等于A、B两点的压强分别加上A、B两点距容器底的那段液体产生的压强,故p甲 > p乙。
故答案为:<;>。先根据ρ=![]() 判断甲、乙两种液体密度的大小,根据p=ρgh判断A、B两点以下的液体对容器底部产生的压强大小后再判断A、B两点处的压强大小;根据p=ρgh和A、B两点压强的大小判断两种液体密度的大小,再根据p=ρgh判断A、B两点以下的液体对容器底部产生的压强大小后再判断全部液体对容器底部产生的压强。
判断甲、乙两种液体密度的大小,根据p=ρgh判断A、B两点以下的液体对容器底部产生的压强大小后再判断A、B两点处的压强大小;根据p=ρgh和A、B两点压强的大小判断两种液体密度的大小,再根据p=ρgh判断A、B两点以下的液体对容器底部产生的压强大小后再判断全部液体对容器底部产生的压强。

练习册系列答案
相关题目