题目内容
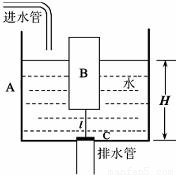
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问(1)请求出水箱中的水深H与轻杆L的函数关系.
(2)当L为多长时,进水管不管进水多长时间也无法把阀门C打开

【答案】分析:仔细读题,明确题意:
(1)当浮筒B所受的浮力大于B的重力与杆的拉力之和时才能将阀门打开,设浮筒B浸入水中深度至少为h时阀门C刚好被打开,根据受力分析与浮力的计算公式求出h,则H=h+d+L;
(2)当浮筒B全部浸没时浮力仍小于或等于B的重力与杆的拉力之和时,不管进水多长时间都无法把阀门C打开;由(1)中H与L的关系以及H≤30cm+L+d,求出L的长度.
解答: 解:由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;
解:由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;
(1)设浮筒B浸入水中的深度至少为h时阀门C刚好被打开;
方法一:
以B为研究对象,受力分析如图甲所示:F浮=GB+F拉
以C为研究对象,受力分析如图乙所示:F拉′=F压
因为F拉=F拉′,所以F浮=GB+F压
即:ρ水gS1h=mBg+ρ水gS2(h+L)
代入数据解得:h=5+L
则水深为:H=h+L+d
即:H=2L+6cm
方法二:
以B和C整体作为研究对象ρg(H-L-d)S1-ρg(H-d)S2=mg
解得: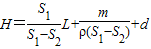
代入数据得:H=2L+6cm
(2)根据题意可知:
H≤30cm+L+d
H≤60cm
H=2L+6cm
由以上3式的L≤25cm
答:(1)水箱中的水深H与轻杆L的函数关系是:H=2L+6cm
(2)当L≤25cm时,进水管不管进水多长时间也无法把阀门C打开.
点评:考查(1)对物体进行受力情况分析.(2)液体内部压强公式.(3)压强的定义式.(4)阿基米德原理.(5)运用物理知识解决生产、生活中实际问题的能力. 综合性强,难度大.
(1)当浮筒B所受的浮力大于B的重力与杆的拉力之和时才能将阀门打开,设浮筒B浸入水中深度至少为h时阀门C刚好被打开,根据受力分析与浮力的计算公式求出h,则H=h+d+L;
(2)当浮筒B全部浸没时浮力仍小于或等于B的重力与杆的拉力之和时,不管进水多长时间都无法把阀门C打开;由(1)中H与L的关系以及H≤30cm+L+d,求出L的长度.
解答:
 解:由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;
解:由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;(1)设浮筒B浸入水中的深度至少为h时阀门C刚好被打开;
方法一:
以B为研究对象,受力分析如图甲所示:F浮=GB+F拉
以C为研究对象,受力分析如图乙所示:F拉′=F压
因为F拉=F拉′,所以F浮=GB+F压
即:ρ水gS1h=mBg+ρ水gS2(h+L)
代入数据解得:h=5+L
则水深为:H=h+L+d
即:H=2L+6cm
方法二:
以B和C整体作为研究对象ρg(H-L-d)S1-ρg(H-d)S2=mg
解得:
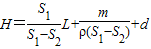
代入数据得:H=2L+6cm
(2)根据题意可知:
H≤30cm+L+d
H≤60cm
H=2L+6cm
由以上3式的L≤25cm
答:(1)水箱中的水深H与轻杆L的函数关系是:H=2L+6cm
(2)当L≤25cm时,进水管不管进水多长时间也无法把阀门C打开.
点评:考查(1)对物体进行受力情况分析.(2)液体内部压强公式.(3)压强的定义式.(4)阿基米德原理.(5)运用物理知识解决生产、生活中实际问题的能力. 综合性强,难度大.

练习册系列答案
相关题目
 某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个边长为50cm的正方体;浮筒B是一个质量为0.2kg的空心圆柱体,其底面积SB为80cm2,高为35cm;放水阀门C是一个质量可忽略的圆柱体,其底面积Sc为55cm2,厚度d为1.5cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻绳与浮筒相连,绳的长度l为10cm.请你计算出水箱中的水深H至少为多少时,浮筒B刚好能将放水阀门C打开?
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个边长为50cm的正方体;浮筒B是一个质量为0.2kg的空心圆柱体,其底面积SB为80cm2,高为35cm;放水阀门C是一个质量可忽略的圆柱体,其底面积Sc为55cm2,厚度d为1.5cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻绳与浮筒相连,绳的长度l为10cm.请你计算出水箱中的水深H至少为多少时,浮筒B刚好能将放水阀门C打开? 某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问 某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问