题目内容
 (2009?大兴区一模)如图所示电路,电源电压U总和灯丝电阻不变.当开关S1断开,S2闭合时,电压表的示数为U,电流表的示数为0.2A;当开关S1闭合,S2断开时,灯泡L正常发光,它此时的实际功率为1.6W,电流表的示数为I′;当两个开关都断开时,电压表的示数为U″,电流表的示数为I″.如果U:U″=4:9,I′:I″=8:3.求
(2009?大兴区一模)如图所示电路,电源电压U总和灯丝电阻不变.当开关S1断开,S2闭合时,电压表的示数为U,电流表的示数为0.2A;当开关S1闭合,S2断开时,灯泡L正常发光,它此时的实际功率为1.6W,电流表的示数为I′;当两个开关都断开时,电压表的示数为U″,电流表的示数为I″.如果U:U″=4:9,I′:I″=8:3.求(1)R2与RL之比.
(2)小灯泡的额定电压.
(3)三个状态中电路的总功率最小时,电阻R1消耗的电功率.
分析:先画出三种情况的等效电路图:
(1)根据电源的电压不变和串联电路的特点以及欧姆定律求出三电阻之间的关系,再根据欧姆定律结合电压表的比值表示出图1和图3中的电流,再根据电源的电压不变得出等式,联立等式即可得出三电阻之间的关系;
(2)根据电源的电压不变和电阻之间的关系求出图1和图2中的电流关系,进一步求出图2中的电流,图2中灯泡正常发光结合P=UI表示出灯泡的电功率即可求出灯泡的额定电压;
(3)由P=
可知,图丙中电路中的电阻最大,电路消耗的总功率最小,根据P=I2R表示出电阻R1消耗的电功率结合电流、电阻关系即可得出答案.
(1)根据电源的电压不变和串联电路的特点以及欧姆定律求出三电阻之间的关系,再根据欧姆定律结合电压表的比值表示出图1和图3中的电流,再根据电源的电压不变得出等式,联立等式即可得出三电阻之间的关系;
(2)根据电源的电压不变和电阻之间的关系求出图1和图2中的电流关系,进一步求出图2中的电流,图2中灯泡正常发光结合P=UI表示出灯泡的电功率即可求出灯泡的额定电压;
(3)由P=
| U2 |
| R |
解答:解:S1断开,S2闭合时,等效电路图如图甲;S1闭合,S2断开时,等效电路图如图乙;S1、S2都断开时,等效电路图如图丙.
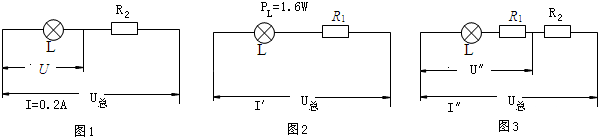
(1)∵电源的电压一定,
∴图2和图3中:
=
=
,
整理可得:RL+R1=
R2------------①
图1中的电流I=
,图3中的电流I″=
,
∵U:U″=4:9,
∴U=I(RL+R2)=I″(RL+R1+R2),
即
(RL+R2)=
(RL+R1+R2)=
×(
R2+R2)=6U,
整理可得:R2=5RL,
代入①式可得:R1=2RL;
(2)图1和图2中:
=
=
=
,
∴I′=2I=2×0.2A=0.4A,
∵P=UI,且灯泡正常发光,
∴灯泡的额定电压:
U额=
=
=4V;
(3)由P=
可知,图丙电路消耗的总功率最小,
∵
=
,R1=2RL,
∴P1=(I″)2×R1=(
I′)2×2RL=
×(I′)2RL=
×1.6W=0.45W.
答:(1)R2与RL之比为5:1;
(2)小灯泡的额定电压为4V;
(3)三个状态中电路的总功率最小时,电阻R1消耗的功率为0.45W.

(1)∵电源的电压一定,
∴图2和图3中:
| I′ |
| I″ |
| RL+R1+R2 |
| RL+R1 |
| 8 |
| 3 |
整理可得:RL+R1=
| 3 |
| 5 |
图1中的电流I=
| U |
| RL |
| U″ |
| R1+RL |
∵U:U″=4:9,
∴U=I(RL+R2)=I″(RL+R1+R2),
即
| U |
| RL |
| U″ |
| R1+RL |
| ||
|
| 3 |
| 5 |
整理可得:R2=5RL,
代入①式可得:R1=2RL;
(2)图1和图2中:
| I |
| I′ |
| RL+R1 |
| RL+R2 |
| RL+2RL |
| RL+5RL |
| 1 |
| 2 |
∴I′=2I=2×0.2A=0.4A,
∵P=UI,且灯泡正常发光,
∴灯泡的额定电压:
U额=
| PL |
| I′ |
| 1.6W |
| 0.4A |
(3)由P=
| U2 |
| R |
∵
| I′ |
| I″ |
| 8 |
| 3 |
∴P1=(I″)2×R1=(
| 3 |
| 8 |
| 9 |
| 32 |
| 9 |
| 32 |
答:(1)R2与RL之比为5:1;
(2)小灯泡的额定电压为4V;
(3)三个状态中电路的总功率最小时,电阻R1消耗的功率为0.45W.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活应用,关键是画出三种情况的等效电路图和利用好电源的电压不变这一条件.

练习册系列答案
相关题目
 (2009?大兴区一模)如图所示,根据透镜前后的入射光线和折射光线,在虚框中填上适当的透镜.
(2009?大兴区一模)如图所示,根据透镜前后的入射光线和折射光线,在虚框中填上适当的透镜. (2009?大兴区一模)将密度为0.6×103kg/m3,长20cm的柱形物块缓缓浸入盛满水的溢水杯中,水的深度为10cm,待物快静止时,从杯中溢出重0.49N的水,如图所示,求:
(2009?大兴区一模)将密度为0.6×103kg/m3,长20cm的柱形物块缓缓浸入盛满水的溢水杯中,水的深度为10cm,待物快静止时,从杯中溢出重0.49N的水,如图所示,求: