题目内容
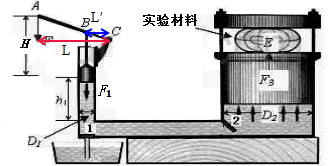
 小娟同学根据佛山正在创建的高新材料产业园需要,设计了一个通过强大压力改变材料内部结构和强度的实验装置.实验原理如图所示,左边圆柱形容器内液体直径和小活塞直径均为D1,右边大圆柱容器内液体直经和大活塞直径均为D2.
小娟同学根据佛山正在创建的高新材料产业园需要,设计了一个通过强大压力改变材料内部结构和强度的实验装置.实验原理如图所示,左边圆柱形容器内液体直径和小活塞直径均为D1,右边大圆柱容器内液体直经和大活塞直径均为D2.(1)图中ABC是
省力
省力
杠杆,当A点受到向下的力作用时阀门1和阀门2的开闭情况如图所示.当A点受到向上的力作用时,阀门2处在闭合
闭合
(填“闭合”或“打开”)状态.(2)小活塞产生向下的作用力为F1,若两活塞下端受到液体的压强相等,则作用在大活塞上的力F2大小为多少?
(3)如何通过改变实验装置才能使实验材料上获得更大的作用力(至少写出两种方法).
分析:(1)分析ABC杠杆动力臂和阻力臂的大小关系,动力臂大于阻力臂为省力杠杆,动力臂小于阻力臂为费力杠杆,动力臂等于阻力臂为等臂杠杆;当A点受到向上的力作用时,活塞上移,阀门1打开,阀门2关闭,液体被压入柱形容器内;
(2)由帕斯卡原理可知,加在密闭液体的压强能大小不变的向各个方向传递,所以两活塞受到的压强相等,即:
=
,据此求出作用在大活塞上的力F2大小;
(3)设大活塞上升的高度为h2,由于这个过程中装置内的液体体积恒定,所以小活塞向下扫过的体积与大活塞向上扫过的体积相等,即V1=V2,可求大活塞上升高度h2,
此装置的有用功W有用=F3h2,总功W总=FH,根据效率公式求此实验装置的机械效率;
为使实验材料获得更大的作用力,可以从增大动力、增大大活塞与小活塞面积的比值、减小摩擦、减小大活塞的重力等方面分析回答.
(2)由帕斯卡原理可知,加在密闭液体的压强能大小不变的向各个方向传递,所以两活塞受到的压强相等,即:
| F1 |
| S1 |
| F2 |
| S2 |
(3)设大活塞上升的高度为h2,由于这个过程中装置内的液体体积恒定,所以小活塞向下扫过的体积与大活塞向上扫过的体积相等,即V1=V2,可求大活塞上升高度h2,
此装置的有用功W有用=F3h2,总功W总=FH,根据效率公式求此实验装置的机械效率;
为使实验材料获得更大的作用力,可以从增大动力、增大大活塞与小活塞面积的比值、减小摩擦、减小大活塞的重力等方面分析回答.
解答:解:
(1)由图可知,动力臂L大于阻力臂L′,ABC是省力杠杆;
当A点受到向上的力作用时,活塞上移,阀门1打开,阀门2关闭,液体被压入柱形容器内;
(2)∵两活塞受到的压强相等,p1=p2,
即:
=
,
=
;
∴F2=
F1;
(3)设大活塞上升的高度为h2,小活塞向下扫过的体积与大活塞向上扫过的体积相等,即V1=V2,
则:π(
D1)2h1=π(
D2)2h2,
所以h2=
h1;
此装置的有用功:
W有用=F3h2=
h1F3,
总功W总=FH,
η=
=
;
使实验材料获得更大的作用力,可以采用的方法:
①加大作用在杠杆上的杠杆上的力F;
②增加大活塞与小活塞面积的比值;
③减少摩擦;
④减少大活塞自身的重力.
故答案为:(1)省力;闭合;
(2)作用在大活塞上的力F2大小为
F1;
(3)此实验装置的机械效率为;①加大作用在杠杆上的杠杆上的力F、②增加大活塞与小活塞面积的比值可以使实验材料上获得更大的作用力.
(1)由图可知,动力臂L大于阻力臂L′,ABC是省力杠杆;
当A点受到向上的力作用时,活塞上移,阀门1打开,阀门2关闭,液体被压入柱形容器内;

(2)∵两活塞受到的压强相等,p1=p2,
即:
| F1 |
| S1 |
| F2 |
| S2 |
| F1 | ||
π(
|
| F2 | ||
π(
|
∴F2=
| ||
|
(3)设大活塞上升的高度为h2,小活塞向下扫过的体积与大活塞向上扫过的体积相等,即V1=V2,
则:π(
| 1 |
| 2 |
| 1 |
| 2 |
所以h2=
| ||
|
此装置的有用功:
W有用=F3h2=
| ||
|
总功W总=FH,
η=
| W有用 |
| W总 |
| D12h1F2 |
| D22Fh |
使实验材料获得更大的作用力,可以采用的方法:
①加大作用在杠杆上的杠杆上的力F;
②增加大活塞与小活塞面积的比值;
③减少摩擦;
④减少大活塞自身的重力.
故答案为:(1)省力;闭合;
(2)作用在大活塞上的力F2大小为
| ||
|
(3)此实验装置的机械效率为;①加大作用在杠杆上的杠杆上的力F、②增加大活塞与小活塞面积的比值可以使实验材料上获得更大的作用力.
点评:本题考查了杠杆平衡条件的应用、帕斯卡原理的应用、机械效率的计算,综合性强、比较复杂;在对本题的阅读过程中如果能按把一个复杂的过程分解成以上几个阶段,则会使复杂问题变得更加简单.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目

