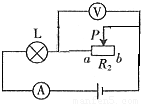
题目内容
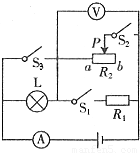
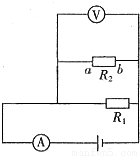
在如图所示的电路中,电源电压和灯泡电阻不变,电阻R1=12Ω,灯L标有“6V 12W”的字样,电流表量程为0~3A,电压表量程为0~15V,滑动变阻器R2上标有“2.5A”的字样.(1)只闭合S1,电流表的示数为0.6A,求电源电压;
(2)当闭合S1、S2和S3,并将滑片P移到b端时,电流表的示数为1.2A,求滑动变阻器R2的最大阻值;
(3)只闭合S2时,求电路总功率的最大值.
【答案】分析:(1)只闭合S1时,灯L与R1串联;由灯泡的铭牌可知额定电压和额定功率,根据R=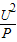 求出灯泡的电阻;根据电阻的串联和欧姆定律求出电源的电压.
求出灯泡的电阻;根据电阻的串联和欧姆定律求出电源的电压.
(2)当闭合S1、S2和S3时,灯L短路,R1与R2并联,电流表测干路电流;根据并联电路的电压特点和欧姆定律求出通过R1的电流,根据并联电路的电流特点求出通过滑动变阻器的电流,再根据欧姆定律求出滑动变阻器的最大阻值.
(3)只闭合S2时,灯泡L与R2串联;先根据I=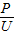 求出灯泡的额定电流,然后与滑动变阻器允许通过的最大电流和电流表的量程确定电路中的最大电流,再根据串联电路的分压特点和电源的电压判断此时电压表是否安全,最后根据P=UI求出电路总功率的最大值.
求出灯泡的额定电流,然后与滑动变阻器允许通过的最大电流和电流表的量程确定电路中的最大电流,再根据串联电路的分压特点和电源的电压判断此时电压表是否安全,最后根据P=UI求出电路总功率的最大值.
解答:解:(1)只闭合S1时,灯L与R1串联,I=0.6A;
灯泡的电阻:
RL= =
=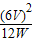 =3Ω,
=3Ω,
电源电压:
U=I(R1+RL)=0.6A×(12Ω+3Ω)=9V.
(2)当闭合S1、S2和S3时,灯L短路,R1与R2并联,I′=1.2A;
通过R1的电流:
I1=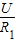 =
=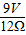 =0.75A,
=0.75A,
滑动变阻器的最大阻值:
Rab=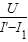 =
=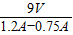 =20Ω.
=20Ω.
(3)只闭合S2时,灯泡L与R2串联,
灯泡L的额定电流:
I额=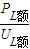 =
=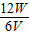 =2A,
=2A,
∵电流表选择的量程为0~3A,滑动变阻器允许通过的最大电流为2.5A,
∴电路中允许通过的最大电流I最大=2A;
电压表的量程为0~15V,而电源电压只有9V,所以电压始终是安全的;
由此可得出电路总功率的最大值为P=UI最大=9V×2A=18W.
答:(1)电源电压为9V;
(2)滑动变阻器的最大阻值为20Ω;
(3)只闭合S2时,电路总功率的最大值为18W.
点评:本题考查了串联电路和并联电路的特点以及欧姆定律、电功率公式的灵活运用,关键是根据灯泡的额定电流和滑动变阻器允许的最大电流以及电流表的量程确定只闭合S2时电路中的最大电流.
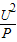 求出灯泡的电阻;根据电阻的串联和欧姆定律求出电源的电压.
求出灯泡的电阻;根据电阻的串联和欧姆定律求出电源的电压.(2)当闭合S1、S2和S3时,灯L短路,R1与R2并联,电流表测干路电流;根据并联电路的电压特点和欧姆定律求出通过R1的电流,根据并联电路的电流特点求出通过滑动变阻器的电流,再根据欧姆定律求出滑动变阻器的最大阻值.
(3)只闭合S2时,灯泡L与R2串联;先根据I=
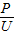 求出灯泡的额定电流,然后与滑动变阻器允许通过的最大电流和电流表的量程确定电路中的最大电流,再根据串联电路的分压特点和电源的电压判断此时电压表是否安全,最后根据P=UI求出电路总功率的最大值.
求出灯泡的额定电流,然后与滑动变阻器允许通过的最大电流和电流表的量程确定电路中的最大电流,再根据串联电路的分压特点和电源的电压判断此时电压表是否安全,最后根据P=UI求出电路总功率的最大值.解答:解:(1)只闭合S1时,灯L与R1串联,I=0.6A;

灯泡的电阻:
RL=
 =
=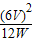 =3Ω,
=3Ω,电源电压:
U=I(R1+RL)=0.6A×(12Ω+3Ω)=9V.
(2)当闭合S1、S2和S3时,灯L短路,R1与R2并联,I′=1.2A;

通过R1的电流:
I1=
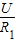 =
=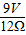 =0.75A,
=0.75A,滑动变阻器的最大阻值:
Rab=
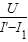 =
=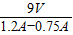 =20Ω.
=20Ω.(3)只闭合S2时,灯泡L与R2串联,

灯泡L的额定电流:
I额=
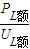 =
=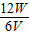 =2A,
=2A,∵电流表选择的量程为0~3A,滑动变阻器允许通过的最大电流为2.5A,
∴电路中允许通过的最大电流I最大=2A;
电压表的量程为0~15V,而电源电压只有9V,所以电压始终是安全的;
由此可得出电路总功率的最大值为P=UI最大=9V×2A=18W.
答:(1)电源电压为9V;
(2)滑动变阻器的最大阻值为20Ω;
(3)只闭合S2时,电路总功率的最大值为18W.
点评:本题考查了串联电路和并联电路的特点以及欧姆定律、电功率公式的灵活运用,关键是根据灯泡的额定电流和滑动变阻器允许的最大电流以及电流表的量程确定只闭合S2时电路中的最大电流.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
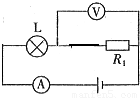
 在如图所示的电路中,开关S闭合后,小灯泡L1L2均正常发光,则下列说法中正确的是( )
在如图所示的电路中,开关S闭合后,小灯泡L1L2均正常发光,则下列说法中正确的是( ) (2011?杨浦区二模)在如图所示的电路中,电源电压保持不变,当电键S由断开到闭合时,电压表V的示数将
(2011?杨浦区二模)在如图所示的电路中,电源电压保持不变,当电键S由断开到闭合时,电压表V的示数将 (2012?南通模拟)在如图所示的电路中,R1=10Ω,R2=20Ω,闭合开关后,电流表的示数为0.3A.求:
(2012?南通模拟)在如图所示的电路中,R1=10Ω,R2=20Ω,闭合开关后,电流表的示数为0.3A.求: 在如图所示的电路中,AB是一段电阻丝,当开关闭合,导线夹由B向A移动的过程中,接入电路的电阻的变化情况是( )
在如图所示的电路中,AB是一段电阻丝,当开关闭合,导线夹由B向A移动的过程中,接入电路的电阻的变化情况是( ) 在如图所示的电路中,小灯泡和电铃采用的是
在如图所示的电路中,小灯泡和电铃采用的是