题目内容
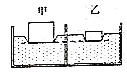
【题目】如图所示,质量分布均匀的实心正方体A和B分别置于高度差为h的水平地面上。物体A的密度为1125千克/米3,物体B的质量为9千克。求:

(1)若物体A的体积为8×10﹣3米3,求物体A的质量mA;
(2)若物体B的边长为0.3米,求物体B对水平地面的压强pB;
(3)若A的边长为2h,且A、B它们对地面的压力相等,现将A、B两正方体沿水平方向截去高度相等的一部分,使它们剩余部分对水平地面的压强相等,求截去的高度△h(△h的值用h表示)。
【答案】(1)9kg;(2)980Pa;(3)1.58 h。
【解析】
(1)根据ρ=![]() 知道,物体A的质量是:mA=ρAVA=1125kg/m3×8×10﹣3m3=9kg;
知道,物体A的质量是:mA=ρAVA=1125kg/m3×8×10﹣3m3=9kg;
(2)物体B对水平地面的压力是:F=GB=mBg=9kg×9.8N/kg=88.2N,
物体B对水平地面的压强是:pB=![]() =980Pa;
=980Pa;
(3)A的边长为2h,则由图可知B的边长为3h,
原来A、B它们对地面的压力相等,即FA=FB,所以,GA=GB;
根据G=mg和ρ=![]() 知道,ρA(2h)3g=ρB(3h)3g,所以,
知道,ρA(2h)3g=ρB(3h)3g,所以,![]() ;
;
将A、B两正方体沿水平方向截去高度相等的一部分,剩余部分对水平地面的压强相等,
所以有:pA′=pB′,
因为![]() =ρgh,设截去高度为△h,
=ρgh,设截去高度为△h,
则ρAg(2h﹣△h)=ρBg(3h﹣△h),解得△h=![]() h≈1.58 h。
h≈1.58 h。

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目