题目内容
如图所示（滑轮组的绕绳未画出），人以600N的力向下拉动绕在滑轮组的绳子一端10s，使绳端向下移动了1.5m、重物匀速上升了0.5m，已知滑轮组的机械效率为70%（g=10N/kg）．（1）人的拉力所做的功是多少？
（2）拉力的功率是多大？
（3）被吊起的重物重力多大？
（4）按题意画出滑轮组的绕绳．
分析：（1）已知F=600N，s=1.5m；可利用W总=Fs求得拉力所做的功；
（2）已知拉力所做的功和t=10s，利用P=
求得；
（3）根据S=nh得到：动滑轮上绳子段数n；
结合机械效率的公式η=
求出重物的重力；
（3）根据动滑轮上绳子段数n，结合滑轮组使用时“奇动偶定”的特点，设计一个符合要求的滑轮组的绳子绕法．
（2）已知拉力所做的功和t=10s，利用P=
| W |
| t |
（3）根据S=nh得到：动滑轮上绳子段数n；
结合机械效率的公式η=
| G |
| nF |
（3）根据动滑轮上绳子段数n，结合滑轮组使用时“奇动偶定”的特点，设计一个符合要求的滑轮组的绳子绕法．
解答：解：（1）拉力所做的功W总=Fs=600N×1.5m=900J；
（2）拉力的功率P=
=
=90W．
（3）∵S=nh；∴n=
=
=3；
∵η=
=
=
=
，
∴G=ηnF=70%×3×600N=1260N；
（4）根据n=3，即动滑轮上绳子段数是3股；则绳子的固定端应从动滑轮上开始缠绕，如图：
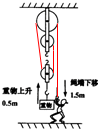
答：（1）人的拉力所做的功是900J；
（2）拉力的功率是90W．
（3）被吊起的重物重力为1260N；
（4）图略．
（2）拉力的功率P=
| W总 |
| t |
| 900J |
| 10s |
（3）∵S=nh；∴n=
| S |
| h |
| 1.5m |
| 0.5m |
∵η=
| W有用 |
| W总 |
| Gh |
| Fs |
| Gh |
| F?nh |
| G |
| nF |
∴G=ηnF=70%×3×600N=1260N；
（4）根据n=3，即动滑轮上绳子段数是3股；则绳子的固定端应从动滑轮上开始缠绕，如图：
答：（1）人的拉力所做的功是900J；
（2）拉力的功率是90W．
（3）被吊起的重物重力为1260N；
（4）图略．
点评：本题虽然考查滑轮组的机械效率，但注意机械效率公式η=
的应用，缠绕滑轮组的绳子时一定结合“奇动偶定”的特点来缠绕．
| G |
| nF |
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
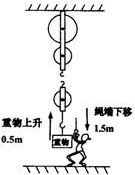如图所示（滑轮组的绕绳未画出），人以600N的力向下拉动绕在滑轮组的绳子一端10秒，使绳端向下移动了1.5m、重物匀速上升了0.5m，已知滑轮组的机械效率为70%（g=10N/kg）．
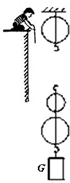（2012?荔湾区一模）如图所示（滑轮组的绕绳未完全画出），滑轮组下方挂一个重为400N的重物G，人向上拉动绕在滑轮组的绳子一端10s，使绳端向上移动了1.6m，重物匀速上升了0.4m，已知滑轮组的机械效率为80%．
如图所示（滑轮组的绕绳未画出），人以600N的力向下拉动绕在滑轮组的绳子一端，10秒使绳端向下移动了1.5m、重物匀速上升了0.5m，已知滑轮组的机械效率为80%（g=10N/kg）．请按题意画出滑轮组的绕绳．并计算人的拉力的功率是
（2013?通州区二模）如图所示（滑轮组的绕绳未画出），质量为60kg的工人师傅利用最省力的方式先后搬运水平地面上的圆柱形物体A和物体B．物体A的底面积为SA，密度为ρA，高度为h1；物体B的底面积为SB，密度为ρB，高度为h2．运送货物A时，工人用力F1匀速拉绳，地面对工人的支持力为N1，滑轮组的机械效率为η1；运送货物B时，工人用力F2匀速拉绳的功率为P2，物体B以0.1m/s的速度匀速上升，地面对工人的支持力为N2，机械效率η2=80%．已知：5N1=4N2，5SA=4SB，8ρA=7ρB，2hA=5hB，不计绳的质量，不计滑轮与轴的摩擦．（g=10N/kg）求：