题目内容
(2012?乌兰察布)如图1所示,某工程队在一次施工作业中,以恒定速度沿竖直方向将质量为5×103kg的圆柱形实心工件从深水中吊起至距水面某一高度.绳子作用在工件上端的拉力F的功率P随工件上升高度h变化的图象如图2所示,不计水的阻力(ρ水=1.0×103kg/m3,g取10N/kg),求:
(1)工件上升的速度大小?
(2)当工件露出水面的1/2时所受的浮力大小?
(3)工件的横截面积S是多大?

(1)工件上升的速度大小?
(2)当工件露出水面的1/2时所受的浮力大小?
(3)工件的横截面积S是多大?

分析:(1)由P-h图象求出工件离开水面后拉力的功率,对工件进行受力分析,由平衡条件求出拉力大小,最后由功率的变形公式v=
求出工件的速度;
(2)由P-h图象求出工件完全浸没在水中时拉力的功率,由功率的变形公式F=
求出拉力,然后对工件进行受力分析,由平衡条件求出工件受到的浮力,最后求出工件露出水面的
时所受的浮力大小;
(3)由图象求出工件的高度,由浮力公式的变形公式求出工件的体积,最后求出工件的横截面积.
| P |
| F |
(2)由P-h图象求出工件完全浸没在水中时拉力的功率,由功率的变形公式F=
| P |
| v |
| 1 |
| 2 |
(3)由图象求出工件的高度,由浮力公式的变形公式求出工件的体积,最后求出工件的横截面积.
解答:解:(1)由P-h图象可知:工件离开水面后拉力F1的功率P1=20kW=2×104W,
工件离开水面后,受竖直向下的重力G、竖直向上的拉力F1用而做匀速运动,处于平衡状态,
由平衡条件得:F1=G=mg=5×103kg×10N/kg=5×104N,
工件匀速上升的速度v=
=
=0.4m/s,
答:工件上升的速度是0.4m/s.
(2)由P-h图象可知:工件全部在水中时拉力F2的功率P2=16kW=1.6×104W,
此时拉力大小为F2=
=
=4×104N,
工件完全浸没在水中时,受竖直向下的重力G、竖直向上的拉力F2、竖直向上的浮力F浮作用,
工件做匀速直线运动,处于平衡状态,由平衡条件得:F2+F浮=G,
则F浮=G-F2=5×104N-4×104N=1×104N,
工件有
露出水面时所受浮力F浮/=
F浮=
×1×104N=5×103N,
答:工件露出水面的
时所受的浮力为5000N.
(3)由P-h图象可知工件高h=12m-10m=2m;
工件的体积V物=V排=
=
=1m3,
工件的横截面积S=
=
=0.5m2,
答:工件的横截面积S是0.5m2.
工件离开水面后,受竖直向下的重力G、竖直向上的拉力F1用而做匀速运动,处于平衡状态,
由平衡条件得:F1=G=mg=5×103kg×10N/kg=5×104N,
工件匀速上升的速度v=
| P1 |
| F1 |
| 2×104W |
| 5×104N |
答:工件上升的速度是0.4m/s.
(2)由P-h图象可知:工件全部在水中时拉力F2的功率P2=16kW=1.6×104W,
此时拉力大小为F2=
| P2 |
| v |
| 1.6×104W |
| 0.4m/s |
工件完全浸没在水中时,受竖直向下的重力G、竖直向上的拉力F2、竖直向上的浮力F浮作用,
工件做匀速直线运动,处于平衡状态,由平衡条件得:F2+F浮=G,
则F浮=G-F2=5×104N-4×104N=1×104N,
工件有
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:工件露出水面的
| 1 |
| 2 |
(3)由P-h图象可知工件高h=12m-10m=2m;
工件的体积V物=V排=
| F浮 |
| ρ水g |
| 1×104N |
| 103kg/m3×10N/kg |
工件的横截面积S=
| V物 |
| h |
| 1m3 |
| 2m |
答:工件的横截面积S是0.5m2.
点评:本题是一道计算题,主要考查了:求物体的速度、物体所受的浮力、物体的横截面积,本题难度较大,是一道难题;
由P-h图象获取足够的信息是正确解题的前提与关键;要加强由图象获取信息能力的培养.
由P-h图象获取足够的信息是正确解题的前提与关键;要加强由图象获取信息能力的培养.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
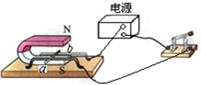 (2012?乌兰察布)关于如图所示的实验装置,下列说法正确的是( )
(2012?乌兰察布)关于如图所示的实验装置,下列说法正确的是( )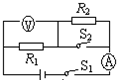 (2012?乌兰察布)如图所示的电路,电源电压保持不变,闭合开关S1、S2,电压表示数为3V,电流表示数为0.3A,断开S2后,电压表示数为2V,则下列判断正确的是( )
(2012?乌兰察布)如图所示的电路,电源电压保持不变,闭合开关S1、S2,电压表示数为3V,电流表示数为0.3A,断开S2后,电压表示数为2V,则下列判断正确的是( )