题目内容
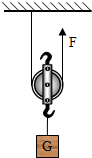
 如图所示,用1.2N拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m,所用时间为4s.
如图所示,用1.2N拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m,所用时间为4s.(1)此过程中拉力的功率为
0.06
0.06
W.(2)将物重由2N不断增大,它的机械效率随着
增大,但总小于100%
增大,但总小于100%
.分析:(1)已知拉力的大小和物体升高的距离以及动滑轮上绳子的段数,根据公式W=Fs可求拉力做的功,还知道所用的时间,根据公式P=
可求拉力的功率;
(2)当物重为2N时的机械效率已经求出,根据公式η=
=
=
=
可知,物体重力越大,机械效率越高,但总小于100%.
| W |
| t |
(2)当物重为2N时的机械效率已经求出,根据公式η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额 |
| Gh |
| Gh+G动h |
| G |
| G+G动 |
解答:解:(1)拉力移动距离:s=2h=2×0.1m=0.2m,
拉力做的总功W总=Fs═1.2N×0.2m=0.24J,
拉力的功率P=
=
=0.06W;
(2)根据公式η=
=
=
=
=
可知,当物体重力增大时,机械效率随之增大,但总小于100%,
故答案为:(1)0.06;(2)增大,但总小于100%.
拉力做的总功W总=Fs═1.2N×0.2m=0.24J,
拉力的功率P=
| W总 |
| t |
| 0.24J |
| 4s |
(2)根据公式η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额 |
| Gh |
| Gh+G动h |
| G |
| G+G动 |
| 1 | ||
1+
|
故答案为:(1)0.06;(2)增大,但总小于100%.
点评:本题考查总功、功率、机械效率等的计算,关键是公式及其变形的灵活运用,还要知道机械效率随物体重力的增加而增加,但不会大于1,因为有用功始终小于总功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m所用时间为4s.
如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m所用时间为4s. (2013?松北区二模)如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m所用时间为4s 此过程中拉力的功率为
(2013?松北区二模)如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m所用时间为4s 此过程中拉力的功率为 如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m所用时间为4s,此过程中拉力的功率为
如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升0.1m所用时间为4s,此过程中拉力的功率为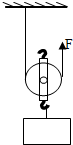 (2011?景德镇模拟)如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升10cm所用时间为4s,关于此过程,以下说法正确的是( )
(2011?景德镇模拟)如图所示,用1.2N的拉力沿竖直方向匀速拉起重为2N的物体,物体上升10cm所用时间为4s,关于此过程,以下说法正确的是( )