题目内容
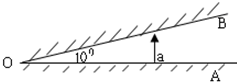
如图所示,两平面镜A和B成10°夹角交于O点,自A镜上a点处垂直A镜射出一条光线,此光线在两镜间经
8
8
次反射后不再与镜面相遇.设两镜面足够长.
分析:当光线的传播方向与平面镜平行时,两者不再相遇,由此入手确定答案.
解答:解:发生第一次反射时,根据三角形的内角和为180°、两个镜面间的夹角为10°,可以求得此时入射光线与镜面的夹角为70°,此时的入射角为10°,根据光的反射规律可知,此时的反射角也为10°,即此时的反射光线与上面平面镜的夹角为100°;
同样可以利用三角形的内角和为180°,可以求出这条反射光线以与下面的平面镜成70°夹角射向下面的平面镜发生第二次反射.
根据光的反射规律可以推出第二次反射时的反射光线与下面的平面镜的夹角与入射光线与镜面的夹角相等,也为70°,经过两次反射后,光线由最初的与平面镜的夹角为90°变为70°.
以此类推,每经过两次反射,出射光线与下面的平面镜的夹角减小20°.当经过8次反射后,出射光线与下面的平面镜成10°角射出.此时的出射光线与上面的平面镜平行,所以不再相遇.
故答案为8次.
同样可以利用三角形的内角和为180°,可以求出这条反射光线以与下面的平面镜成70°夹角射向下面的平面镜发生第二次反射.
根据光的反射规律可以推出第二次反射时的反射光线与下面的平面镜的夹角与入射光线与镜面的夹角相等,也为70°,经过两次反射后,光线由最初的与平面镜的夹角为90°变为70°.
以此类推,每经过两次反射,出射光线与下面的平面镜的夹角减小20°.当经过8次反射后,出射光线与下面的平面镜成10°角射出.此时的出射光线与上面的平面镜平行,所以不再相遇.
故答案为8次.
点评:明确不再相遇的含义是解决此题的入手点.
通过前两次的反射,明确角度的变换规律是难点.
通过前两次的反射,明确角度的变换规律是难点.

练习册系列答案
相关题目
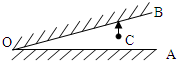 如图所示,两平面镜A和B成15°夹角交于O点,从C点处垂直于A镜射出一条光线,此光线在两镜间经多次反射后不再与镜面相遇.试问:有几次反射?而最后一次反射发生在哪个镜面上?(镜面足够长)( )
如图所示,两平面镜A和B成15°夹角交于O点,从C点处垂直于A镜射出一条光线,此光线在两镜间经多次反射后不再与镜面相遇.试问:有几次反射?而最后一次反射发生在哪个镜面上?(镜面足够长)( ) 如图所示,两平面镜A和B之间的夹角为9°自平面镜B上的某点P射出一条与B镜面成β角的光线,在β角由0°至180°范围内(不包括0°)连续变化的过程中,发现当β取某角度时,光线经镜面一次或多次反射后,恰好能返回到P点,则符合该要求的β的个数有( )
如图所示,两平面镜A和B之间的夹角为9°自平面镜B上的某点P射出一条与B镜面成β角的光线,在β角由0°至180°范围内(不包括0°)连续变化的过程中,发现当β取某角度时,光线经镜面一次或多次反射后,恰好能返回到P点,则符合该要求的β的个数有( )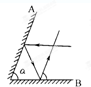 如图所示,两平面镜A和B相交成角a,若入射光线跟B镜面平行,经镜面反射后,射出的光线与A平行,则角a为( )
如图所示,两平面镜A和B相交成角a,若入射光线跟B镜面平行,经镜面反射后,射出的光线与A平行,则角a为( )