题目内容
 (2013?海淀区一模)如图所示,电源两端电压保持不变,R1、R2为定值电阻,开关S3始终闭合.闭合开关S1、断开开关S2,滑动变阻器的滑片置于某位置M时(图中未标出),滑动变阻器的阻值为RM,电流表的示数为I1,滑动变阻器的电功率PM为0.4W.保持开关S1闭合、开关S2断开,将滑动变阻器的滑片置于某位置N时(图中未标出),滑动变阻器的阻值为RN,电流表的示数为I2,电压表的示数为U1,滑动变阻器的电功率PN仍为0.4W.断开开关S1、闭合开关S2,滑动变阻器的滑片仍置于位置N时,电压表的示数变为U2.已知I1:I2=2:1,U1:U2=7:9.求:
(2013?海淀区一模)如图所示,电源两端电压保持不变,R1、R2为定值电阻,开关S3始终闭合.闭合开关S1、断开开关S2,滑动变阻器的滑片置于某位置M时(图中未标出),滑动变阻器的阻值为RM,电流表的示数为I1,滑动变阻器的电功率PM为0.4W.保持开关S1闭合、开关S2断开,将滑动变阻器的滑片置于某位置N时(图中未标出),滑动变阻器的阻值为RN,电流表的示数为I2,电压表的示数为U1,滑动变阻器的电功率PN仍为0.4W.断开开关S1、闭合开关S2,滑动变阻器的滑片仍置于位置N时,电压表的示数变为U2.已知I1:I2=2:1,U1:U2=7:9.求:(1)滑动变阻器接入电路的阻值RM与RN之比;
(2)定值电阻R1与R2的阻值之比;
(3)改变开关状态和调节滑动变阻器的阻值,使电路的电功率最大,求出电路的最大电功率.
分析:分别画出四种情况下(①当闭合开关S1、断开开关S2,滑动变阻器的滑片在某位置M时;②当闭合开关S1、断开开关S2,滑动变阻器的滑片在某位置N时;③当断开开关S1、闭合开关S2,滑动变阻器滑片仍在某位置N时;④当电路消耗的电功率最大时)的等效电路图,根据题目提供条件分别求解.
解答:解:
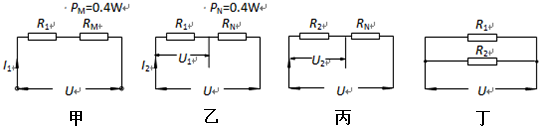
当闭合开关S1、断开开关S2,滑动变阻器的滑片在某位置M时,等效电路如图甲所示;
当闭合开关S1、断开开关S2,滑动变阻器的滑片在某位置N时,等效电路如图乙所示;
当断开开关S1、闭合开关S2,滑动变阻器滑片仍在某位置N时,等效电路如图丙所示;
当电路消耗的电功率最大时,等效电路如图丁所示.
(1)∵PM=I12RM=0.4W,PN=I22RN=0.4W
∴
=
=
=
(2)由于电源电压不变,I1(R1+RM)=I2(R1+RN)
∴
=
=
,
又∵
=
,
∴
=
,
=
,
在图乙中,
=
=
,
又∵
=
,
∴
=
在图丙中,
=
=
,
∴
=
∴
=
;
(3)PM=I12RM=(
)2×RM=
=0.4W,
∴
=3.6W,
∵
=
,
=
,
∴
=
,
∴P=
+
=
+
=
×3.6W=3W.
答:(1)滑动变阻器接入电路的阻值RM与RN之比为1:4;
(2)定值电阻R1与R2的阻值之比为2:3;
(3)电路的最大电功率为3W.
当闭合开关S1、断开开关S2,滑动变阻器的滑片在某位置M时,等效电路如图甲所示;
当闭合开关S1、断开开关S2,滑动变阻器的滑片在某位置N时,等效电路如图乙所示;
当断开开关S1、闭合开关S2,滑动变阻器滑片仍在某位置N时,等效电路如图丙所示;
当电路消耗的电功率最大时,等效电路如图丁所示.

(1)∵PM=I12RM=0.4W,PN=I22RN=0.4W
∴
| RM |
| RN |
| ||||
|
| ||
|
| 1 |
| 4 |
(2)由于电源电压不变,I1(R1+RM)=I2(R1+RN)
∴
| I1 |
| I2 |
| R1+RN |
| R1+RM |
| 2 |
| 1 |
又∵
| RM |
| RN |
| 1 |
| 4 |
∴
| R1 |
| RM |
| 2 |
| 1 |
| R1 |
| RN |
| 1 |
| 2 |
在图乙中,
| U1 |
| U |
| R1 |
| R1+RN |
| 1 |
| 3 |
又∵
| U1 |
| U2 |
| 7 |
| 9 |
∴
| U2 |
| U |
| 3 |
| 7 |
在图丙中,
| U2 |
| U |
| R2 |
| R2+RN |
| 3 |
| 7 |
∴
| R2 |
| RN |
| 3 |
| 4 |
∴
| R1 |
| R2 |
| 2 |
| 3 |
(3)PM=I12RM=(
| U |
| R1+RM |
| U2 |
| 9RM |
∴
| U2 |
| RM |
∵
| R1 |
| RM |
| 2 |
| 1 |
| R1 |
| R2 |
| 2 |
| 3 |
∴
| R2 |
| RM |
| 3 |
| 1 |
∴P=
| U2 |
| R1 |
| U2 |
| R2 |
| U2 |
| 2RM |
| U2 |
| 3RM |
| 5 |
| 6 |
答:(1)滑动变阻器接入电路的阻值RM与RN之比为1:4;
(2)定值电阻R1与R2的阻值之比为2:3;
(3)电路的最大电功率为3W.
点评:本题为较复杂的电路动态分析计算题,分析题意画出四种情况下的等效电路图是本题的关键.

练习册系列答案
相关题目

 (2013?海淀区一模)小明想利用一块电流表和一个电阻箱R′测量未知电阻Rx的阻值.他选择了满足实验要求的实验器材,并按照图所示的电路图连接好实验电路.以下是他设计的实验方案,请将实验步骤补充完整,并写出未知电阻Rx阻值的表达式:
(2013?海淀区一模)小明想利用一块电流表和一个电阻箱R′测量未知电阻Rx的阻值.他选择了满足实验要求的实验器材,并按照图所示的电路图连接好实验电路.以下是他设计的实验方案,请将实验步骤补充完整,并写出未知电阻Rx阻值的表达式: