题目内容
【题目】如图所示，电源电压为6V，R1为“40Ω，0.25A”滑动变阻器，R2为“10Ω，0.5A”电阻，电压表量程为0～3V。图中虚线框内接一只“20Ω，0.4A”电阻R（未画出）。已知：①闭合S1和S3 ， 断开S2时，调节R1使其接入电路的阻值为10Ω，此时电路消耗的电功率为1.2W；②断开S3 ， 闭合S1、S2 ， 调节R1使其接入电路的阻值为6Ω，此时电压表的示数为1.0V。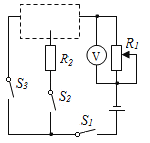
⑴在情形①中，求电路的总阻值；
⑵根据情形①和②，在图中虚线框内将R连入电路；
⑶当闭合所有开关时，为保证电路安全，求滑动变阻器R1接入电路的阻值范围。
【答案】解：⑴根据P=
可得，在情形①中电路的总阻值：
R总= 
= 
=30Ω；
⑵情形②中，电路中的电流：
I= 
= 
= 
A，
电路中的总电阻：
R总′=
= 
=36Ω，
而R1+R2=6Ω+10Ω=16Ω，
比较可知，R总′＞R1+R2 ， 说明电阻R接在虚线框的右侧，
所以，此时电路应为R1与R2、滑动变阻器R串联组成，虚线框内的电路如下图所示：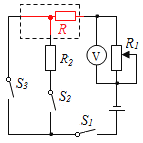
⑶闭合所有开关时，电阻R与滑动变阻器R1串联，电压表测R1两端的电压，
当电路中的电流最大时滑动变阻器接入电路的电阻最小，
因串联电路中各处的电流相等，且滑动变阻器允许通过的最大电流为0.25A，
所以，电路中的最大电流为0.25A，此时电路中的总电阻：
R总″=
= 
=24Ω，
滑动变阻器接入电路中的最小阻值：Rmin=R总″﹣R=24Ω﹣20Ω=4Ω；
当电压表的示数U滑=3V时，滑动变阻器接入电路中的电阻最大，
因串联电路中总电压等于各分电压之和，
所以，R两端的电压：UR=U﹣U滑=6V﹣3V=3V，
此时电路中的电流：
Imin=
= 
=0.15A，
滑动变阻器接入电路中的最大阻值：
R=
= 
=20Ω，
故滑动变阻器接入电路的阻值范围为4Ω～20Ω。
答：⑴在情形①中电路的总阻值为30Ω；⑵虚线框内的电路如上图所示；⑶当闭合所有开关时，为保证电路安全，滑动变阻器接入电路的阻值范围为4Ω～20Ω。
【解析】⑴知道电源的电压和情形①中电路消耗的总功率，根据P= 
求出电路的总阻值；⑵根据串联电路的电流特点和欧姆定律求出电路中的电流，利用欧姆定律求出电路中的总电阻，总电阻大于滑动变阻器接入电路中的电阻和R1的阻值之和，据此可知此时R2应串联在电路中，据此画出虚线框内的电路；⑶闭合所有开关时，电阻R与滑动变阻器R1串联，电压表测R1两端的电压，当电路中的电流最大时滑动变阻器接入电路的电阻最小，根据滑动变阻器和R1允许通过的最大电流确定电路中的最大电流，利用欧姆定律求出电路中的总电阻，利用电阻的串联求出滑动变阻器接入电路中的最小阻值；当电压表的示数最大时，滑动变阻器接入电路中的电阻最大，根据电阻的串联求出R两端的电压，利用串联电路的电流特点和欧姆定律求出滑动变阻器接入电路中的最大阻值，进一步得出滑动变阻器接入电路的阻值范围。
本题考查了串联电路的特点和欧姆定律、电功率公式的应用，关键是根据情形①判断出电阻R2的位置和滑动变阻器接入电路中最大、最小阻值的确定。
【考点精析】根据题目的已知条件，利用欧姆定律及其应用和电功率的计算公式的相关知识可以得到问题的答案，需要掌握欧姆定律的应用： ① 同一个电阻，阻值不变，与电流和电压无关 但加在这个电阻两端的电压增大时，通过的电流也增大．（R=U/I） ② 当电压不变时，电阻越大，则通过的电流就越小．（I=U/R） ③ 当电流一定时，电阻越大，则电阻两端的电压就越大．（U=IR）；计算电功率公式：P =W/t ；P=UI ; 式中单位P→瓦(w)；W→焦；t→秒；U→伏（V）；I→安（A）计算电功率还可用公式：P=I2R和P= U2/R．
