题目内容
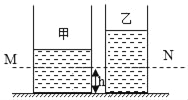
【题目】如图所示,薄壁圆柱形容器甲、乙放在水平面上,甲中盛有深度为5h的水,乙中盛有深度为6h的某液体。求:
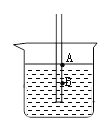
①水面下0.2米深处的压强p水。
在图示水平面MN处两种液体的压强相等,求液体密度ρ液。
③若A容器底面积为2S,B容器底面积为S,问:有没有可能将体积为V的金属球浸没在两液体中后(没有液体溢出),两液体对容器底部的压强p水等于p液?若有可能,请计算V的大小,若无可能,请说明理由。
【答案】1960帕 0.8×103千克/米3 0.67Sh
【解析】
①已知水深,利用p=ρgh计算压强;
②根据p=ρgh和MN处两种液体的压强相等即可求出液体的密度;
③将体积为V的金属球浸没在两液体中,根据液体对容器底的压强相等,结合V=Sh可求出金属球体积的大小。
①水面下0.2米深处的压强为:
p水=ρ水gh=1.0×103kg/m3×9.8N/kg×0.2m=1960Pa;
②因为MN处两种液体的压强相等,即:p水=p液,
根据![]() 可得:ρ水ghM=ρ液ghN,
可得:ρ水ghM=ρ液ghN,
ρ水g(5h-h)=ρ液g(6h-h)
解得液体的密度为:
![]() ;
;
③将体积为V的金属球浸没在两液体中后,此时A容器中水的深度:
![]() ,
,
此时B容器中液体深度:
![]() ,
,
若p水=p液,即:ρ水ghA′=ρ液ghB′,
![]() ,
,
![]()
解得金属球的体积:
![]() 。
。

练习册系列答案
相关题目