题目内容
【题目】如图所示，电源电压恒为24V，灯泡L上标有“12V 6W”字样，滑动变阻器R1的最大阻值为100Ω，电压表量程为0～15V，电流表量程为0～0.6A，图中虚线框内接有一只20Ω的定值电阻R2（未画出）．已知：①闭合S1和S3、断开S2时，调节R1，使其接入电路的阻值为20Ω，此时电路的总功率为14.4W；②闭合S1和S2、断开S3，调节R1，当电压表的示数为15V时，电流表读数为0.22A．
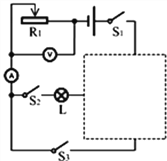
（1）灯泡L正常发光时的阻值为_______Ω，在情形①中，电路的总电阻为________Ω．
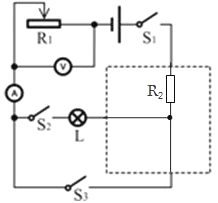
（2）请根据题意在虚线框内画出R2，并使电路完整___．
（3）闭合S1和S2、断开S3，移动滑动变阻器的滑片P的过程中，求小灯泡的最小功率____．
【答案】 24 40 见解析 1.012W
【解析】（1）由题知，灯泡的额定电压和额定功率，由P＝
可得灯泡电阻：
RL＝
＝24Ω；情形①中，闭合S1和S3、断开S2时，R1与串联虚线框部分串联，
由P＝U2计算此时电路的总电阻：R＝
＝40Ω，（2）在情形①中，R1使其接入电路的阻值为20Ω，由串联电路的电阻特点可知，虚线框部分连入电阻的阻值为：R框＝R-R1＝40Ω-20Ω＝20Ω，情形②中，闭合S1和S2、断开S3，虚线框部分、灯泡、R1串联，电压表测R1两端两端电压，电流表测电路中电流，此时灯泡与虚线框部分的总电压：U′＝U-U1＝24V-15V＝9V，由串联电路特点和欧姆定律可得，此时灯泡与虚线框部分接入电路的总电阻值：RL+R框′＝
≈40.9Ω，由①②两种情形知，电阻R2即要在闭合S3时连入电路，又要在闭合S2时与灯串联，由此可知R2的位置如图所示：
（3）闭合S1和S2，断开S3，R2、灯泡、R1串联，当滑动变阻器两端电压最大时，电路中电阻最大，电流最小时，灯泡功率最小，此时R2两端电压：U2＝IR2＝0.22A×20Ω＝4.4V，灯泡两端电压：UL＝U总-U2-U1＝24V-15V-4.4V＝4.6V，由P＝UI可得灯泡的最小功率：P＝ULI′＝4.6V×0.22A＝1.012W．
