题目内容
【题目】如图所示,电源电压恒为24V,小灯泡标有“6V、3W”字样,定值电阻R2的阻值为24Ω,当S闭合,S1、S2都断开且滑片P移到滑动变阻器的中点时,灯L正常发光.
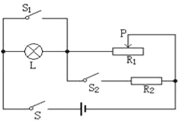
(1)灯泡L的电阻是多少?
(2)滑动变阻器的最大阻值是多少?
(3)当S1、S2都闭合时,调节滑动变阻器,使整个电路消耗的总功率最小,这个最小值是多少?
【答案】(1)灯泡的电阻为12Ω;(2)滑动变阻器的最大电阻为72Ω;(3)电路中消耗的最小功率为32W.
【解析】试题分析:(1)由灯泡的铭牌信息可知灯泡的额定功率及额定电压,则由功率公式可求得灯泡的电阻;
(2)当S闭合,S1、S2都断开时,电路中灯泡及滑动变阻器串联,则由串联电路的欧姆定律可得出滑动变阻器两端的电压,由欧姆定律可求得滑动变阻器的接入电阻,由题意可知,最大阻值与接入电阻的关系,则可知最大阻值;
(3)当S1、S2都闭合时,R1与R2并联,因电源电压不变,则可知当电路电流最小时消耗的功率最小,即应使滑片滑到右端时,电路中消耗功率最小,则由并联电路的规律求得总电阻,由功率公式可求得最小功率.
解:(1)由功率公式:P=![]() 得:
得:
灯泡的电阻:
R=![]() =
=![]() =12Ω;
=12Ω;
(2)当S闭合,S1、S2都断开,L与R1串联,P位于中点L正常发光时
U1=U﹣U额=24V﹣6V=18V;
I=![]() =
=![]() =0.5A;
=0.5A;
R1中=![]() =
=![]() =36Ω;
=36Ω;
R1最大=2R1中=2×36Ω=72Ω;
(3)当S、S1、S2都闭合,R1、R2并联且滑片置于最右端时,电路消耗功率最小
R总=![]() =
=![]() =18Ω;
=18Ω;
P最小=![]() =
=![]() =32W;
=32W;
答:(1)灯泡的电阻为12Ω;(2)滑动变阻器的最大电阻为72Ω;(3)电路中消耗的最小功率为32W.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目