题目内容
某同学用圆柱形容器制作了一个测量物体质量的装置,它的底部较重,可以竖直漂浮在水面,其总质量为0.21kg、底面积为3×10-3m2.不放物体时,与水面所对应位置处的刻度线的标定值m为“0”,如图甲所示,求该装置所受的浮力F1.若在该装置中放入一个体积为1.5×10-5m3的物块,圆柱形容器的底部在水面下的深度h=0.11m,如图乙所示,求该装置受到的浮力F2和此时与水面所对应位置处的刻度线的标定值m.(友情提示:一定要画受力分析图哟!)
【答案】分析:以圆柱形容器为研究对象和以圆柱形容器和物块的整体为研究对象进行受力分析;
(1)先根据G=mg求出该装置的重力,物体静止时处于平衡状态,受到的浮力和容器自身的重力相等,根据二力平衡条件求出该装置所受的浮力F1.
(2)在该装置中放入物体后,先求出容器排开水的体积,根据阿基米德原理求出受到的浮力,此时容器受到的浮力等于容器自重和物体的重力之和,进一步求出物块的重力,根据G=mg求出物体的质量即为此时与水面所对应位置处的刻度线的标定值.
解答:解:以圆柱形容器为研究对象,受力分析如图甲所示;以圆柱形容器和物块的整体为研究对象,受力分析如图乙所示;
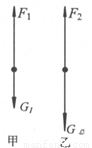
(1)该装置的重力:
G=mg=0.21kg×10N/kg=2.1N,
由图甲,根据二力平衡条件可知:
F1=G=2.1N.
(2)该装置排开水的体积为:
V排=Sh=3×10-3m2×0.11m=3.3×10-4m3,
所受的浮力为:
F2=ρ水gV排=1.0×103kg/m3×10N/kg×3.3×10-4m3=3.3N,
由图乙,根据二力平衡条件可知:
G总=F2=3.3N.
物块的重力:
G物=G总-G=3.3N-2.1N=1.2N.
物块的质量:
m物=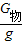 =
=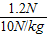 =0.12kg=120g.
=0.12kg=120g.
所以与水面所对应位置处的刻度线应标为120g.
答:图甲所示该装置所受的浮力F1为2.1N,图乙所示该装置受到的浮力F2为3.3N,此时与水面所对应位置处的刻度线的标定值为120g.
点评:本题考查了学生对密度公式、重力公式、阿基米德原理掌握和运用,解题时要注意所给的提示即利用二力平衡条件进行解答,本题的综合性较强,有一定的难度.
(1)先根据G=mg求出该装置的重力,物体静止时处于平衡状态,受到的浮力和容器自身的重力相等,根据二力平衡条件求出该装置所受的浮力F1.
(2)在该装置中放入物体后,先求出容器排开水的体积,根据阿基米德原理求出受到的浮力,此时容器受到的浮力等于容器自重和物体的重力之和,进一步求出物块的重力,根据G=mg求出物体的质量即为此时与水面所对应位置处的刻度线的标定值.
解答:解:以圆柱形容器为研究对象,受力分析如图甲所示;以圆柱形容器和物块的整体为研究对象,受力分析如图乙所示;

(1)该装置的重力:
G=mg=0.21kg×10N/kg=2.1N,
由图甲,根据二力平衡条件可知:
F1=G=2.1N.
(2)该装置排开水的体积为:
V排=Sh=3×10-3m2×0.11m=3.3×10-4m3,
所受的浮力为:
F2=ρ水gV排=1.0×103kg/m3×10N/kg×3.3×10-4m3=3.3N,
由图乙,根据二力平衡条件可知:
G总=F2=3.3N.
物块的重力:
G物=G总-G=3.3N-2.1N=1.2N.
物块的质量:
m物=
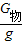 =
=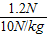 =0.12kg=120g.
=0.12kg=120g.所以与水面所对应位置处的刻度线应标为120g.
答:图甲所示该装置所受的浮力F1为2.1N,图乙所示该装置受到的浮力F2为3.3N,此时与水面所对应位置处的刻度线的标定值为120g.
点评:本题考查了学生对密度公式、重力公式、阿基米德原理掌握和运用,解题时要注意所给的提示即利用二力平衡条件进行解答,本题的综合性较强,有一定的难度.

练习册系列答案
相关题目
 (2011?陕西)某同学用圆柱形容器制作了一个测量物体质量的装置.它的底部较重,可以竖直漂浮在水面,总质量为0.21kg,底面积为3×10-3m2,不放物体时,在与水面所对应位置处标为质量的“0”刻度线,如图.请解答下列问题(g取10N/kg)
(2011?陕西)某同学用圆柱形容器制作了一个测量物体质量的装置.它的底部较重,可以竖直漂浮在水面,总质量为0.21kg,底面积为3×10-3m2,不放物体时,在与水面所对应位置处标为质量的“0”刻度线,如图.请解答下列问题(g取10N/kg) 某同学用圆柱形容器制作了一个测量物体质量的装置,它的底部较重,可以竖直漂浮在水面,其总质量为0.21kg、底面积为3×10-3m2.不放物体时,与水面所对应位置处的刻度线的标定值m0为“0”,如图甲所示,求该装置所受的浮力F1.若在该装置中放入一个体积为1.5×10-5m3的物块,圆柱形容器的底部在水面下的深度h=0.11m,如图乙所示,求该装置受到的浮力F2和此时与水面所对应位置处的刻度线的标定值m.(友情提示:一定要画受力分析图哟!)
某同学用圆柱形容器制作了一个测量物体质量的装置,它的底部较重,可以竖直漂浮在水面,其总质量为0.21kg、底面积为3×10-3m2.不放物体时,与水面所对应位置处的刻度线的标定值m0为“0”,如图甲所示,求该装置所受的浮力F1.若在该装置中放入一个体积为1.5×10-5m3的物块,圆柱形容器的底部在水面下的深度h=0.11m,如图乙所示,求该装置受到的浮力F2和此时与水面所对应位置处的刻度线的标定值m.(友情提示:一定要画受力分析图哟!) 某同学用圆柱形容器制作了一个测量物体质量的装置,它的底部较重,可以竖直漂浮在水面,其总质量为0.21kg、底面积为3×10-3m2.不放物体时,与水面所对应位置处的刻度线的标定值量为“0”,如图甲所示,在该装置中放一物块A,圆柱形容器的底部在水面下的深度h=0.11m,如图乙所示(g取10N/kg).则下列判断不正确的是( )
某同学用圆柱形容器制作了一个测量物体质量的装置,它的底部较重,可以竖直漂浮在水面,其总质量为0.21kg、底面积为3×10-3m2.不放物体时,与水面所对应位置处的刻度线的标定值量为“0”,如图甲所示,在该装置中放一物块A,圆柱形容器的底部在水面下的深度h=0.11m,如图乙所示(g取10N/kg).则下列判断不正确的是( )
