题目内容
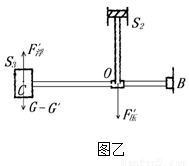
某工厂设计了一个蓄水池,如图25所示,水源A罐的液面高度h1=3m,且保持不变。罐底有一个小出水口,面积为S1,S1=0.1m2.孔下通过一个截面积为S2活塞与杠杆BC相连, S2=0.24m2。杠杆可绕B端上下转动,另一端有一个中空的圆柱体浮子,横截面积为S3,S3=0.8m2,BO是杠杆总长的 。原设计打算当杠杆水平时,浮子浸入水深为h2, h2=0.7m,活塞恰好能赌住出水口,但在使用时发现,活塞离出水口尚有一小段距离时,浮子便不再上浮,此时浮子浸入水深为h3,h3=1m,为了使活塞自动堵住出水口,只得将浮子的质量减去一部分,设减去的质量为m′。(g取10N/kg,杠杆水平时,认为BO仍是杠杆总长的
。原设计打算当杠杆水平时,浮子浸入水深为h2, h2=0.7m,活塞恰好能赌住出水口,但在使用时发现,活塞离出水口尚有一小段距离时,浮子便不再上浮,此时浮子浸入水深为h3,h3=1m,为了使活塞自动堵住出水口,只得将浮子的质量减去一部分,设减去的质量为m′。(g取10N/kg,杠杆水平时,认为BO仍是杠杆总长的 ,活塞及连杆和杠杆的质量均不计,杠杆所受浮力不计,浮子浸入水中体积变化引起的蓄水池液面变化忽略不计。)试求
,活塞及连杆和杠杆的质量均不计,杠杆所受浮力不计,浮子浸入水中体积变化引起的蓄水池液面变化忽略不计。)试求

(1)活塞应上升的高度是多少;
(2)浮子应减去质量m′是多少。
略
【解析】设浮子原来重力为G,杠杆长为。浮子减重G′后,由倾斜变为水平,如图5所示,
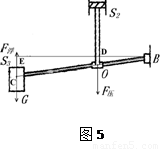
杠杆C端上升高度为hEC=h3-h2, (1分)
根据数学知识,三角形BDO相似于三角形BEC
所以
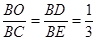
活塞上升高度DO段长为Δh=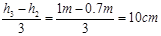 。 (1分)
。 (1分)
活塞减重前,杠杆平衡时,
以浮子为研究对象,C端受到的合力为F浮-G=(S3 h3ρ水g-G)
O点受到的力为F压=ρ水gS2(h1+Δh)
根据杠杆平衡有:
(F浮-G)BE=F压BD
(S3 h3ρ水g-G)=ρ水gS2(h1+Δh)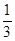 (1) (1分)
(1) (1分)
浮子减重后,杠杆平衡时,以杠杆为研究对象,进行受力分析:
C端受到的合力为
F′浮-(G-G′)= 〔S3h2ρ水g-( G-G′)〕
O点受到的力为F´压=ρ水gS1h1
根据杠杆平衡有:
〔S3h2ρ水g-( G-G′)〕=ρ水gS1h1 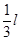 (2)
(1分)
(2)
(1分)
解上面的联立方程,可得
G´=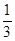 ρ水g〔S1h1+3S3(h3-h2)-S2(h1+
ρ水g〔S1h1+3S3(h3-h2)-S2(h1+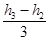 〕
(1分)
〕
(1分)
带入已知数据解得:G′=920N (1分)
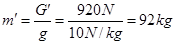
注:正确画出受力分析图 (1分)

 春雨教育同步作文系列答案
春雨教育同步作文系列答案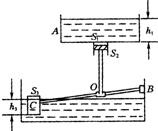 某工厂设计了一个蓄水池(如图所示),水源A罐的夜面高度h1保持不变.罐底有一个小出水口,面积为S1.孔下通过一个截面积为S2活塞与杠杆BC相连.杠杆可绕B端上下转动,另一端有一个中空的圆柱形浮子,横截面积为S3,BO是杠杆总长的
某工厂设计了一个蓄水池(如图所示),水源A罐的夜面高度h1保持不变.罐底有一个小出水口,面积为S1.孔下通过一个截面积为S2活塞与杠杆BC相连.杠杆可绕B端上下转动,另一端有一个中空的圆柱形浮子,横截面积为S3,BO是杠杆总长的 (2011?昌平区一模)某工厂设计了一个蓄水池,如图所示,水源A罐的液面高度h1=3m,且保持不变.罐底有一个小出水口,面积为S1,S1=0.1m2.孔下通过一个截面积为S2活塞与杠杆BC相连,S2=0.24m2.杠杆可绕B端上下转动,另一端有一个中空的圆柱体浮子,横截面积为S3,S3=0.8m2,BO是杠杆总长
(2011?昌平区一模)某工厂设计了一个蓄水池,如图所示,水源A罐的液面高度h1=3m,且保持不变.罐底有一个小出水口,面积为S1,S1=0.1m2.孔下通过一个截面积为S2活塞与杠杆BC相连,S2=0.24m2.杠杆可绕B端上下转动,另一端有一个中空的圆柱体浮子,横截面积为S3,S3=0.8m2,BO是杠杆总长
 .原设计打算当杠杆水平时,浮子浸入水深为h2,h2=0.7m,活塞恰好能赌住出水口,但在使用时发现,活塞离出水口尚有一小段距离时,浮子便不再上浮,此时浮子浸入水深为h3,h3=1m,为了使活塞自动堵住出水口,只得将浮子的质量减去一部分,设减去的质量为m′.(g取10N/kg,杠杆水平时,认为BO仍是杠杆总长
.原设计打算当杠杆水平时,浮子浸入水深为h2,h2=0.7m,活塞恰好能赌住出水口,但在使用时发现,活塞离出水口尚有一小段距离时,浮子便不再上浮,此时浮子浸入水深为h3,h3=1m,为了使活塞自动堵住出水口,只得将浮子的质量减去一部分,设减去的质量为m′.(g取10N/kg,杠杆水平时,认为BO仍是杠杆总长 ,活塞及连杆和杠杆的质量均不计,杠杆所受浮力不计,浮子浸入水中体积变化引起的蓄水池液面变化忽略不计.)试求
,活塞及连杆和杠杆的质量均不计,杠杆所受浮力不计,浮子浸入水中体积变化引起的蓄水池液面变化忽略不计.)试求