题目内容
 如图,一卡车车厢底板距地面1.5m高,小明把一块3m长的钢板AB搭在车厢底板上,构成一个斜面.他通过这个斜面,用F=600N的力,把一个大木箱由B处推到A处,已知木箱重为1000N.
如图,一卡车车厢底板距地面1.5m高,小明把一块3m长的钢板AB搭在车厢底板上,构成一个斜面.他通过这个斜面,用F=600N的力,把一个大木箱由B处推到A处,已知木箱重为1000N.(1)把木箱由B处推到A处,用了30s时间,求推力的功率.
(2)这个过程中,斜面的机械效率是多少?(结果保留一位小数)
(3)求木箱在斜面上受到的摩擦力.
分析:(1)知道木箱在推力的作用下移动的距离和推力的大小,可利用公式W=FS计算出推力做的总功,又知道做功的时间,可利用公式P=
计算出推力的功率.
(2)知道木箱的重力和木箱升高的高度,可利用公式W=Gh计算出克服重力做的有用功,再利用公式η=
计算出斜面的机械效率.
(3)人做的额外功是人克服摩擦力做功,等于总功减去额外功,再利用W额=fs求摩擦力.
| W总 |
| t |
(2)知道木箱的重力和木箱升高的高度,可利用公式W=Gh计算出克服重力做的有用功,再利用公式η=
| W有用 |
| W总 |
(3)人做的额外功是人克服摩擦力做功,等于总功减去额外功,再利用W额=fs求摩擦力.
解答:解;
(1)∵F=600N,S=3m,
∴推力做的总功为:W总=FS=600N×3m=1800J,
而t=30s,
∴推力的功率为;P=
=
=60W.
(2)∵G=1000N,h=1.5m,
∴克服重力做的有用功为:W有用=Gh=1000N×1.5m=1500J,
斜面的机械效率为:η=
=
≈83.3%.
(3)小明做的额外功为:W=W总-W有用=1800J-1500J=300J,
∴摩擦力的大小为:f=
=
=100N.
答:(1)推力的功率为60W.
(2)斜面的机械效率是83.3%.
(3)木箱在斜面上受到的摩擦力为100N.
(1)∵F=600N,S=3m,
∴推力做的总功为:W总=FS=600N×3m=1800J,
而t=30s,
∴推力的功率为;P=
| W总 |
| t |
| 1800J |
| 30s |
(2)∵G=1000N,h=1.5m,
∴克服重力做的有用功为:W有用=Gh=1000N×1.5m=1500J,
斜面的机械效率为:η=
| W有用 |
| W总 |
| 1500J |
| 1800J |
(3)小明做的额外功为:W=W总-W有用=1800J-1500J=300J,
∴摩擦力的大小为:f=
| W额外 |
| S |
| 300J |
| 3m |
答:(1)推力的功率为60W.
(2)斜面的机械效率是83.3%.
(3)木箱在斜面上受到的摩擦力为100N.
点评:本题考查了总功、有用功、斜面机械效率和功率的计算,以及对公式变形的理解和应用,解答此题的关键是要知道使用斜面有用功(提升重物做功)、总功(推力做功)、额外功(克服摩擦做功)的意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
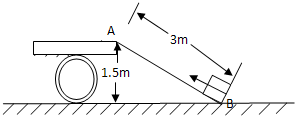 如图,一卡车车厢底板距地面1.5m高,小明把一块3m长的钢板AB搭在车厢底板上,构成一个斜面.他通过这个斜面,用F=600N的力,把一个大木箱由B处推到A处,已知木箱重为100kg,木箱底部与地面的接触面积是100cm2.求:
如图,一卡车车厢底板距地面1.5m高,小明把一块3m长的钢板AB搭在车厢底板上,构成一个斜面.他通过这个斜面,用F=600N的力,把一个大木箱由B处推到A处,已知木箱重为100kg,木箱底部与地面的接触面积是100cm2.求: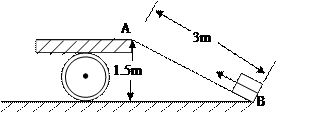
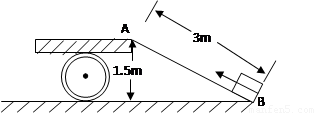
 如图,一卡车车厢底板距地面1.5m高,小明把一块3m长的钢板AB搭在车厢底板上,构成一个斜面.他通过这个斜面,用F=600N的力,把一个大木箱由B处推到A处,已知木箱重为100kg,木箱底部与地面的接触面积是100cm2.求:
如图,一卡车车厢底板距地面1.5m高,小明把一块3m长的钢板AB搭在车厢底板上,构成一个斜面.他通过这个斜面,用F=600N的力,把一个大木箱由B处推到A处,已知木箱重为100kg,木箱底部与地面的接触面积是100cm2.求: