题目内容
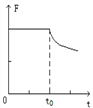
【题目】在装有水的烧杯中漂浮着甲、乙两个实心球,两球露出水面的体积相等,已知两球的质量m甲>m乙.当往水中慢慢倒入酒精并缓慢搅拌的过程中,甲球的浮力大小F与时间t的变化关系如图所示.则关于乙球开始沉没于液面之下的时刻t’与t0关系正确的是
A. t’>t0 B. t’=t0 C. t’<t0 D. 乙球不可能沉入液面下
【答案】A
【解析】由题意和图示可知,甲球受到的浮力先不变,随着酒精的加入,混合液体的密度逐渐减小,浮力减小,当浮力小于重力时(液体的密度小于甲球的密度),甲球下沉.
ABC、因为G=mg,且m甲>m乙,所以G甲>G乙,
又甲、乙两个实心球漂浮在水中,
所以F浮甲=G甲,F浮乙=G乙,
则F浮甲>F浮乙,
又因为F浮=ρ液gV排,
所以V排甲>V排乙,
甲和乙露出水面的体积相等,所以甲的体积比乙的体积大;
物体漂浮,所以F浮=G=mg,即ρ水gV排=ρ(V排+V露)g,
则物体的密度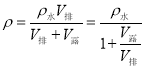 ,因为甲、乙露出部分的体积相等,且V排甲>V排乙,所以ρ甲>ρ乙;
,因为甲、乙露出部分的体积相等,且V排甲>V排乙,所以ρ甲>ρ乙;
又因为甲球的密度较大,故甲球早开始浸没,
因为甲和乙露出水面的体积相同,若乙球能浸没,则甲早浸没于混合液体中,即乙球开始沉没于液面之下的时刻t′大于甲球开始沉没于液面之下的时刻t0,故A正确,BC错误;
D、因为不知道乙和酒精与水混合液的密度大小关系,所以不能判断乙球是否沉入液面下,故D错误.
故选A.

练习册系列答案
相关题目