题目内容
图为发光点S和竖直放置的平面镜的位置情况。根据光的反射定律完成下列两小题:

(1)在图中用光路图作出发光点S的像点S'
(2)推导证明S'点和S点到平面镜距离相等

(1)在图中用光路图作出发光点S的像点S'
(2)推导证明S'点和S点到平面镜距离相等
(1)如图所示 (2)见解析部分
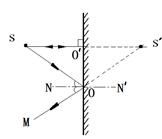

试题分析:(1)平面镜成的是一个正立、等大的虚像,物和像的连线与镜面垂直,物和像到镜面的距离相等,物和像关于镜面对称的。平面镜成像的原理是光的反射,像是由物体的光经镜面反射后,反射光线的反向延长线的交点即为像。从S点任意作两根光线,利用反射定律作出反射光线,把反射光线反射延长,相交于S’,即为S点的像。
(2)要证明像与物到镜面的距离相等,可以利用数学中的全等来证明,证明三角形SO’O与三角形S’O’O全等。
如图甲所示,NN′为法线,SO′为垂直于镜面的入射光线,OM为入射光线SO的反射光线
根据光的反射定律可得:∠ MON=∠SON
又∵∠S′ON′=∠MON(对顶角相等)∴∠S′ON′=∠SON
∵法线NN′与镜面垂直∴∠S′OO′=∠SOO′
又∵ OO′为△′SOO和′△SOO′的公共边
∴Rt△S′OO′≌Rt△SOO′
∴S′O′=SO′

练习册系列答案
相关题目
 、
、 。
。
