题目内容
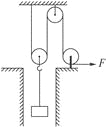
【题目】如图所示,某矿产工人用200N的水平拉力,抓紧绳子的一端,沿水平方向向右运动,在10s内将矿井里质量为32kg的物体提升4m。若不计一切摩擦,求:
(1)矿工在10s内所做的功和他做功的功率;
(2)动滑轮受到的重力;
(3)滑轮组的机械效率。(取g=10N/kg)
【答案】(1)矿工在10s内所做的功为1600J;他做功的功率为160W。
(2)动滑轮受到的重力为80N。
(3)滑轮组的机械效率为80%。
【解析】(1)因为该滑轮组有两段绳子承担物体和动滑轮
所以s=2h=4m×2=8m
所以W总=Fs=200N×8m=1600J
所以P总=W总/t=1600J÷10s=160W。
(2)因为G=mg=32kg×10N/kg=320N
又因为该滑轮组有两段绳子承担物体和动滑轮
所以F=(G物+G滑)/2
所以G滑=2F-G物=200N×2-320N=80N。
(3)W有用=G物h=320N×4m=1280J
所以η=W有/W总=1280J÷1600J=80%。
思路分析:根据滑轮组的性质和W=Fs、P=W/t、η=W有用/W总即可完成该题。根据图中滑轮组的性质可知,s=2h,因为h已知,所以可求出绳子末端移动的距离s,又因拉力已知,根据W=Fs可求出矿工在10s内所做的功,又因时间已知,根据P=W/t可求出他做功的功率。由于不计一切摩擦,所以拉力等于物体和动滑轮总重的1/2,据此求出物体受到的重力,就可求出动滑轮受到的重力。根据以上条件,利用W有=G物h求出有用功,再根据η=W有用/W总就可求出滑轮组的机械效率。

练习册系列答案
相关题目
