题目内容
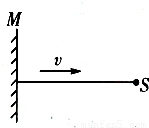
 平面镜M沿水平方向以大小不变的速度v 移向点光源S,运动中镜面始终保持与运动方向成60°角.如图所示,则S在镜中的像S′移动速度的大小和方向( )
平面镜M沿水平方向以大小不变的速度v 移向点光源S,运动中镜面始终保持与运动方向成60°角.如图所示,则S在镜中的像S′移动速度的大小和方向( )分析:平面镜成像的特点:像和物体各对应点到平面镜间距离相等,像和物体各对应点的连线与平面镜垂直,由此可知物接近镜面的速度等于像接近镜面的速度.
解答: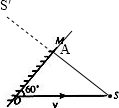 解:如图所示,过S点作出像点S′,
解:如图所示,过S点作出像点S′,
平面镜M沿水平方向以大小不变的速度v 移向点光源S,可知SO=v,
又因为运动中镜面始终保持与运动方向成60°角.所以∠S=30°,所以AO=
v
由勾股定理得SA=
v,这是S移向平面镜的速度,由平面镜成像特点知,S在镜中的像S′移动速度的大小与S移向平面镜的速度相同,即S在镜中的像S′移动速度的大小为
v,方向是沿SS′连线向S移动.
故选D.
 解:如图所示,过S点作出像点S′,
解:如图所示,过S点作出像点S′,平面镜M沿水平方向以大小不变的速度v 移向点光源S,可知SO=v,
又因为运动中镜面始终保持与运动方向成60°角.所以∠S=30°,所以AO=
| 1 |
| 2 |
由勾股定理得SA=
| ||
| 2 |
| 3 |
故选D.
点评:这是一道物理与数学综合题,此题的难度在于利用勾股定理求出SA,本题中学生要明确把平面镜M沿水平方向以大小不变的速度v 当路程来计算.因此此题有一定的难度,并要求学生具备一定的学科综合能力.

练习册系列答案
相关题目
 平面镜M沿水平方向以大小不变的速度v移向点光源S,运动中镜面始终保持与运动方向垂直(如图所示),则S在镜中的像S′移动速度的大小和方向是( )
平面镜M沿水平方向以大小不变的速度v移向点光源S,运动中镜面始终保持与运动方向垂直(如图所示),则S在镜中的像S′移动速度的大小和方向是( )
 v水平向右移动
v水平向右移动 v/2沿SS′连线向S移动
v/2沿SS′连线向S移动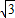 v沿SS′连线向S移动
v沿SS′连线向S移动
 v水平向右移动
v水平向右移动 v/2沿SS′连线向S移动
v/2沿SS′连线向S移动 v沿SS′连线向S移动
v沿SS′连线向S移动