题目内容
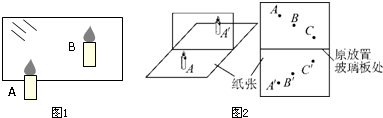
如图1所示,在日常生活中,两个小孩能提起的一桶水,一个大人就能提起来.物理学中将大人对水桶的拉力F称为两小孩对水桶的拉力F1、F2的 ,将F1、F2称为F的 .这是因为 .某学习小组观察到图中两小孩对水桶的拉力方向是倾斜向上的.为了研究这种情况下两小孩对水桶的拉力F1、F2的大小之和是否还等于大人对水桶的拉力F的大小,设计了如图2所示实验.
将橡皮筋一端固定在画板上,另一端拴上细线通过定滑轮悬挂钩码使橡皮筋伸长到O点,记下此时细线对橡皮筋的拉力F大小和方向;然后用两细线互成一定角度通过定滑轮悬挂钩码使橡皮筋仍然伸长到O点,记下此时两细线对橡皮筋的拉力F1、F2大小和方向.

(1)若使用的钩码质量为50克,取g=10N/Kg.上图是某次实验时得到的实物图片,测得两细线间的夹角为90°,请在右边方框(如图3)内分别作出力F、F1、F2的图示.
(2)由实验探究可以得出:
①当F1与F2的方向不同时,它们的大小之和与它们的合力大小 .
②假设保持两根细线分别悬挂4个和3个钩码不变,通过调整两个定滑轮位置,使两根细线的夹角由90°逐渐变为零度,则橡皮筋的伸长量将 ;说明两根细线的拉力F1与F2的合力将 .
③由上述分析可得出:两个力的合力与 有关.
【答案】分析:如果一个力产生的作用效果跟几个力共同产生的作用效果相同,这个力就叫做那几个力的合力,组成合力的每一个力叫做分力.
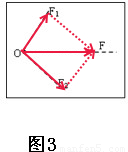
(1)先画出F1、F2的图示,然后利用平行四边形法则画出合力F的图示;
(2)①同一直线上,同方向二力的合力最大,反方向二力的合力最小;
②同一直线上,同方向二力的合力最大;
③根据①②出现的现象分析合力与那些因素有关.
解答:解:两个小孩共同提起一桶水,而大人一个人就可以提起,就是说大人用的力与两个小孩用的力的作用效果相同,大人对水桶的拉力F称为两小孩对水桶的拉力F1、F2的合力,F1、F2称为F的分力.
(1)一个钩码的重力:G=mg=0.05kg×10N/kg=0.5N,
根据图1可知,合力F=5G=5×0.5N=2.5N;
根据图2可知,分力F1=4G=4×0.5N=2N,F2=3G=3×0.5N=1.5N;如下图所示:
(2)①F1+F2=2N+1.5N=3.5N>2.5N,因此当F1与F2的方向不同时,它们的大小之和与它们的合力大小不相等;
②当二力的夹角由90°逐渐变为零度时,合力最大,因此橡皮筋的伸长量增大,说明两根细线的拉力F1与F2的合力将增大;
③根据①②可知,合力的大小与分力的大小和方向都有关系.
故答案为:合力;分力;作用效果相同.
(2)①不相等;②增大;增大;③分力的大小和方向.
点评:本题探究互成角度二力合力的影响因素,知道用等效替代法研究力的合成是本题的解题关键.
(1)先画出F1、F2的图示,然后利用平行四边形法则画出合力F的图示;
(2)①同一直线上,同方向二力的合力最大,反方向二力的合力最小;
②同一直线上,同方向二力的合力最大;
③根据①②出现的现象分析合力与那些因素有关.
解答:解:两个小孩共同提起一桶水,而大人一个人就可以提起,就是说大人用的力与两个小孩用的力的作用效果相同,大人对水桶的拉力F称为两小孩对水桶的拉力F1、F2的合力,F1、F2称为F的分力.
(1)一个钩码的重力:G=mg=0.05kg×10N/kg=0.5N,
根据图1可知,合力F=5G=5×0.5N=2.5N;
根据图2可知,分力F1=4G=4×0.5N=2N,F2=3G=3×0.5N=1.5N;如下图所示:

(2)①F1+F2=2N+1.5N=3.5N>2.5N,因此当F1与F2的方向不同时,它们的大小之和与它们的合力大小不相等;
②当二力的夹角由90°逐渐变为零度时,合力最大,因此橡皮筋的伸长量增大,说明两根细线的拉力F1与F2的合力将增大;
③根据①②可知,合力的大小与分力的大小和方向都有关系.
故答案为:合力;分力;作用效果相同.
(2)①不相等;②增大;增大;③分力的大小和方向.
点评:本题探究互成角度二力合力的影响因素,知道用等效替代法研究力的合成是本题的解题关键.

练习册系列答案
相关题目

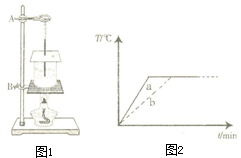 (2013?阜新)在探究“水的沸腾”实验中:
(2013?阜新)在探究“水的沸腾”实验中: