题目内容
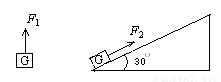
 放在倾角为α斜面上的物体,对斜面的压力与物体重的关系是N=G?cosα,而摩擦力与压力成正比.如图所示,将同一物体,分别用F1、F2的推力,沿接触面粗糙程度相同的AB、AC两斜面从底端用相同时间匀速推到斜面顶端,推力F1、F2所做的功分别为W1、W2,做功的功率分别是P1、P2,下列说法正确的是( )
放在倾角为α斜面上的物体,对斜面的压力与物体重的关系是N=G?cosα,而摩擦力与压力成正比.如图所示,将同一物体,分别用F1、F2的推力,沿接触面粗糙程度相同的AB、AC两斜面从底端用相同时间匀速推到斜面顶端,推力F1、F2所做的功分别为W1、W2,做功的功率分别是P1、P2,下列说法正确的是( )分析:由题意可知:
①从底端用相同时间匀速推到斜面顶端,根据公式P=
可知:只比较拉力所做功的大小关系即可得知.
②将同一物体利用斜面从底端到斜面顶端,物体提升的高度相同,则根据W=Gh可知:利用AB、AC两斜面推力F1、F2所做的有用功相同;
③沿接触面粗糙程度相同的AB、AC两斜面,说明摩擦力由物体对斜面的压力决定,使用斜面的额外功就是由于克服摩擦而产生的,所以比较推力F1、F2所做的功的关系,只需要比较额外功的大小即可.
①从底端用相同时间匀速推到斜面顶端,根据公式P=
| W |
| t |
②将同一物体利用斜面从底端到斜面顶端,物体提升的高度相同,则根据W=Gh可知:利用AB、AC两斜面推力F1、F2所做的有用功相同;
③沿接触面粗糙程度相同的AB、AC两斜面,说明摩擦力由物体对斜面的压力决定,使用斜面的额外功就是由于克服摩擦而产生的,所以比较推力F1、F2所做的功的关系,只需要比较额外功的大小即可.
解答:解:由题意可知:
∵将同一物体利用斜面从底端到斜面顶端,则物体的重力G和提升的高度h相同
∴根据W=Gh可知:W有用1=W有用2;
由图可知:α<β,
∵N1=G?cosα,N2=G?cosβ;
∴N1>N2,
∵摩擦力与压力成正比.
∴摩擦力f1>f2,
由图可知:L1>L2,
∴根据W额=fL可知:W额1=>W额2,
∵W总=W有用+W额;
∴W1>W2,
∵从底端用相同时间匀速推到斜面顶端,则所有时间相同,
∴根据公式P=
可知:P1>P2.
故选B.
∵将同一物体利用斜面从底端到斜面顶端,则物体的重力G和提升的高度h相同
∴根据W=Gh可知:W有用1=W有用2;
由图可知:α<β,
∵N1=G?cosα,N2=G?cosβ;
∴N1>N2,
∵摩擦力与压力成正比.
∴摩擦力f1>f2,
由图可知:L1>L2,
∴根据W额=fL可知:W额1=>W额2,
∵W总=W有用+W额;
∴W1>W2,
∵从底端用相同时间匀速推到斜面顶端,则所有时间相同,
∴根据公式P=
| W |
| t |
故选B.
点评:本题考查斜面的省力情况,物体做功的大小以及做功功率的大小,关键是知道接触面粗糙时,摩擦力不为0,使用斜面的额外功就是由于克服摩擦而产生的,知道根据W额=fL求额外功是本题的关键.

练习册系列答案
相关题目
 30、如图所示,物体G所受到的重力大小为40N.
30、如图所示,物体G所受到的重力大小为40N.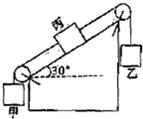 16、如图所示,重3N的甲物体和重12N的乙物体通过细线绕过定滑轮与丙物体连在一起,丙放在倾角为30°的光滑斜面上,整个装置处于静止状态.现将斜面变成粗糙的斜面,乙物体重量变为20N,其余不变,整个装置处于静止状态.则此时丙物体受到的摩擦力大小为
16、如图所示,重3N的甲物体和重12N的乙物体通过细线绕过定滑轮与丙物体连在一起,丙放在倾角为30°的光滑斜面上,整个装置处于静止状态.现将斜面变成粗糙的斜面,乙物体重量变为20N,其余不变,整个装置处于静止状态.则此时丙物体受到的摩擦力大小为 (2006?滨湖区一模)如图所示,小宇同学将重为40N的物体G在拉力F1的作用下沿竖直方向匀速提高0.5m,小丽同学将该物体放在倾角为300的光滑斜面上,用平行于斜面的拉力F2使物体沿斜面匀速向上移动1m,此时拉力F2的大小恰为20N.小宇和小丽所做的功分别为W1和W2,则W1
(2006?滨湖区一模)如图所示,小宇同学将重为40N的物体G在拉力F1的作用下沿竖直方向匀速提高0.5m,小丽同学将该物体放在倾角为300的光滑斜面上,用平行于斜面的拉力F2使物体沿斜面匀速向上移动1m,此时拉力F2的大小恰为20N.小宇和小丽所做的功分别为W1和W2,则W1 (2010?介休市二模)某同学为探究斜面的机械效率,做了如下实验:如图所示,物体G所受到的重力大小为40N.
(2010?介休市二模)某同学为探究斜面的机械效率,做了如下实验:如图所示,物体G所受到的重力大小为40N.