题目内容
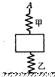
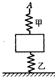 如图所示,甲、乙两根相同的轻弹簧,分别与物块的上下表面相连接,乙弹簧的下端与地面连接.起初甲弹簧处于自由长度,乙弹簧的压缩长度为△L.现用手将甲弹簧缓慢上提,使乙弹簧承受物重的2/3,乙弹簧仍处于压缩状态,那么,甲弹簧的A端应向上提起的距离为
如图所示,甲、乙两根相同的轻弹簧,分别与物块的上下表面相连接,乙弹簧的下端与地面连接.起初甲弹簧处于自由长度,乙弹簧的压缩长度为△L.现用手将甲弹簧缓慢上提,使乙弹簧承受物重的2/3,乙弹簧仍处于压缩状态,那么,甲弹簧的A端应向上提起的距离为| 2 |
| 3 |
| 2 |
| 3 |
分析:(1)根据乙弹簧的受力情况,先求出乙弹簧长度的变化量;
(2)再根据甲弹簧的受力情况,求出甲弹簧长度的变化量;
(3)最后求出甲弹簧A端向上提起的距离.
(2)再根据甲弹簧的受力情况,求出甲弹簧长度的变化量;
(3)最后求出甲弹簧A端向上提起的距离.
解答:解:(1)乙弹簧,一开始,重物压在乙上,乙形变△L,
当压力为重物G的
时,根据胡克定律得:
=
,
所以△L′=
△L,乙弹簧相对于原来的位置上升了△h乙=△L-△L′=
△L.
(2)对于甲弹簧,开始甲弹簧拉力为零,
由于乙弹簧原来受压力为G,后来受压力为
G,则甲弹簧的拉力为
G,
所以甲弹簧上端升高了△h甲=
△L.
(3)甲弹簧的A端应向上提起的距离为△h=△h甲+△h乙=
△L+
△L=
△L.
故答案为:
△L.
当压力为重物G的
| 2 |
| 3 |
| ||
| G |
| △L′ |
| △L |
所以△L′=
| 2 |
| 3 |
| 1 |
| 3 |
(2)对于甲弹簧,开始甲弹簧拉力为零,
由于乙弹簧原来受压力为G,后来受压力为
| 2 |
| 3 |
| 1 |
| 3 |
所以甲弹簧上端升高了△h甲=
| 1 |
| 3 |
(3)甲弹簧的A端应向上提起的距离为△h=△h甲+△h乙=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查了弹簧的弹力与弹簧伸长的关系,解题是要注意,向上拉弹簧甲的时候,弹簧乙也变长,高度要增加,A端上升的高度是甲乙弹簧上升的高度之和.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
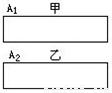
 如图所示,甲、乙两根钢棒,若用甲棒的A1端靠近乙棒的A2端时,有吸引作用若用甲棒的A1端靠近乙棒的中部时没有吸引作用.关于这两根钢棒,以下说法中正确的是( )
如图所示,甲、乙两根钢棒,若用甲棒的A1端靠近乙棒的A2端时,有吸引作用若用甲棒的A1端靠近乙棒的中部时没有吸引作用.关于这两根钢棒,以下说法中正确的是( )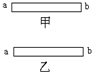 如图所示,甲、乙两根钢棒(外形相同),用甲棒的a端靠近乙棒的b端,有吸引作用,用甲棒的b端靠近乙棒的中部没有吸引作用,关于这两根钢棒,以下说法中正确的是( )
如图所示,甲、乙两根钢棒(外形相同),用甲棒的a端靠近乙棒的b端,有吸引作用,用甲棒的b端靠近乙棒的中部没有吸引作用,关于这两根钢棒,以下说法中正确的是( )