题目内容
一根长2.2m的粗细不均匀的木料，一端放在地面上，抬起它的粗端要用680N的力；若粗端放在地上，抬起它的另一端时需要用420N的力，求：
（1）木料重多少？
（2）木料重心的位置．
（1）木料重多少？
（2）木料重心的位置．
分析：设杠杆的重心位置距杠杆一端的距离，然后根据杠杆平衡的条件列出两个关系式，解之即可．
解答：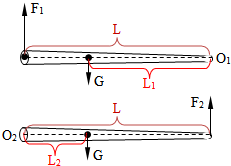
解：如右图：木料的长为 L=2.2m，木料的重心离细端的距离为L1，离粗端的距离为L2；
由杠杆平衡的条件可得：
F1L=GL1，代入数据得：680N×2.2m=G×L1 …①
F2L=GL2，代入数据得：420N×2.2m=G×（2.2m-L1）…②
联立①②，得：
G=1100N，L1=1.36m．
答：（1）木料重1100N；（2）木料重心的位置距细端1.36m．
解：如右图：木料的长为 L=2.2m，木料的重心离细端的距离为L1，离粗端的距离为L2；由杠杆平衡的条件可得：
F1L=GL1，代入数据得：680N×2.2m=G×L1 …①
F2L=GL2，代入数据得：420N×2.2m=G×（2.2m-L1）…②
联立①②，得：
G=1100N，L1=1.36m．
答：（1）木料重1100N；（2）木料重心的位置距细端1.36m．
点评：本题考查杠杆平衡条件的应用，并且会根据杠杆平衡的条件确定杠杆的重心．
练习册系列答案
相关题目