题目内容
不同的材料具有不同的性质,下列关于材料的性质及其应用的说法中,正确的是( )A.机械表中的发条,主要应用其弹性好的特性
B.用橡胶做汽车轮胎,主要应用其硬度大的特性
C.用钢铁做建筑材料,主要应用其导电性好的特性
D.玻璃能按照需要分割成不同的大小和形状,主要应用其硬度大的特性
解答:解:A、机械表中的发条采用钢丝制作,钢丝的弹性好,能把弹性势能转化为动能,故A正确.
B、橡胶在常温下有良好的弹性,能减小汽车的震动与颠簸,同时橡胶做的轮胎耐磨性优异、抗湿滑性好、生热低、曲挠性好,用橡胶做汽车轮胎是利用了橡胶的以上性能,故B错误.
C、用钢铁做建筑材料,应用了钢铁硬度大,承重能力强的性质,故C错误.
D、玻璃能够分割成不同大小和形状,是利用了玻璃可塑性,故D错误.
故选A.
点评:生活中常说的“物尽所用”,指的就是不同的物质按其属性的不同有不同的用处,平时要多留意,多观察,多思考.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案初中物理欧姆定律阶梯训练
欧姆定律
基础知识与基本技能
*1.导体中的电流,跟这段导体 成正比,跟这段导体 成反比。这个结论是德国物理学家 在19世纪初通过实验研究得出的。通常叫做 。它写成公式是 。[2.5]
*2.电流的符号是 ,单位是 ,单位的符号是 ;电压的符号是 ,单位是 ,单位的符号是 ;电阻的符号是 ,单位是 ,单位的符号是 。*3.单位换算:[1.5]24000Ω= kΩ= MΩ 1.1×105V= kV= mV
260mA= A= μA
*4.用 表测出电阻两端的电压,用 表测出通过电阻的电流,根据欧姆定律就可以计算出电阻R,这种测电阻的方法叫 法。此实验的原理是 。[1.5]
**5.装有两节新干电池的手电筒,它的电压是 V。若灯泡的电阻为10Ω,当它正常发光时,通过灯丝的电流约是 。[1.0]
**6.有一导体两端的电压为12V时,通过它的电流为0.2A,它的电阻是 ;当它两端的电压为6V时,它的电阻是 ;当它两端的电压为0V时,它的电阻是 ,通过导体的电流是 。[1.5]
**7.我们利用下列器材研究电流跟电压、电阻之间的关系。按电路图(图15-2)用笔线连接电路(图15-3)。[3.5]
在研究电流跟电压的关系时,应保持 不变,移动变阻器的滑片,改变电阻R两端的 ,测出相应的 。在研究电流跟电阻的关系时,应保持
不变,改变 ,测出相应的 。
**8.下面的表格是“研究电流跟电压、电阻关系”的实验数据记录:[2.5]
电阻R(Ω) | 5 | 10 | 20 |
电流I(A) | 0.4 | 0.2 | 0.1 |
表1电阻R=15Ω 表2 电压U=2V
电压U(V) | 1.5 | 3 | 4.5 |
电流I(A) | 0.1 | 0.2 | 0.3 |
分析表1数据,可得出结论 ;
分析表2数据,可得出结论 。
**9.某导体两端的电压为0.5V时,通过导体的电流是0.1A,那么当电压为1.5V时,通过导体的电流是 A。[1.0]
**10.在研究电流与电阻的关系时,若导体的电阻为20Ω时,电流为0.2A,那么,导体的电阻为 Ω时,通过导体的电流为0.4A。[1.0]
**11.将30Ω的电阻接在一电源的两端,通过电阻的电流是0.3A,若把30Ω的电阻拿走,将10Ω与60Ω的电阻分别接在这个电源的两端,那么通过两电阻的电流分别是( )。[1.5
A.0.9A,0.15A B.0.15A,0.9A C.0.1A,0.6A D.0.6A,0.1A
**12.在研究“电流跟电压、电阻的关系”的实验中,
如图15-4所示,我们先使电阻箱R的电阻取某一值,多次改变滑动变阻器的阻值,记录每一次的 和相应的电流值,得到当电阻不变时,电流跟 成正比的关系;然后多次改变电阻箱R的电阻,调节变阻器的滑片,使每次 保持不变,记录每次电阻箱R的阻值和相应的 值,得到电流跟 成反比的关系。[3.5]
**13.导体的电阻为15Ω,当其两端电压为6V时,通过它的电流是0.4A,若将它两端的电压增加到12V时,通过它的电流为 ,此时该导体的电阻为 。[1.5]
**14.如图15-5所示的电路,是表示滑动变阻器连入电路的四种接法。当滑片向左滑动的过程中,(1)电流表示数变大的是 电路图;(2)电流表的示数变小的是 电路图;(3)电流表的示数不变的是 电路图;(4)不正确的连法是 电路图。[2.5]
**15.判断题:[2.5]
①( )灯泡发光时通过的电量越多,则电流越大
②( )电阻是导体对电流的阻碍作用,所以当导体中没有电流时,导体中就没有电阻了
③( )欧姆就是电阻
④( )某段导体中的电压越大,则对电流的阻碍作用就越大
⑤( )导体长度越长,横截面积越大,则它对电流阻碍作用就越大
⑥( )将两个阻值不同的电阻串联后接在电阻中,则电阻大的通过的电流小
⑦( )由U=IR可知,在并联电路中电阻较大的,它两端的电压也较大
知识的应用**16.下列说法中正确的是( )。[0.5]
A.电流跟电压成正比 B.电流跟电阻成反比
C.在导体的电阻一定时,导体中的电流跟导体两端的电压成正比
D.在导体两端电压一定时,导体中的电流跟导体的电阻成正比
**17.由欧姆定律![]() 推得
推得![]() ,下列说法中正确的是( )。[1.0]
,下列说法中正确的是( )。[1.0]
A.导体的电阻与导体两端电压成正比B.导体的电阻与通过导体的电流成反比
C.导体的电阻是导体本身的属性,等于电压与电流的比值D.以上说法都不对
18.一个灯泡的灯丝的电阻是4Ω,当它两端的电压是2.8V时,求通过灯泡的电流是多少?
**19.通过一个电阻器的电流是0.4A,电阻器的电阻是90Ω,求它们两端的电压是多大?
**20.把一个电热器把它接在家庭电路上,通过它的电流是5A,该电热器的电阻是多少?
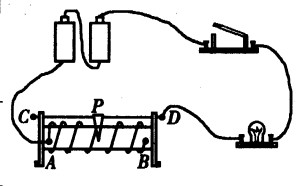

**21.如图15-6,开关合上前,滑动变阻器的滑片P应移至 端。当滑片从中点开始(此时灯泡正常发光)向右移动时,变阻器连入电路的阻值变 ,电路中的电流变 ,灯泡亮度变 。[2.5]
**22.如图15-7电流表A1的示数为0.9A,电流表A2的示数为0.5A,则通过电阻R1的电流是 ,通过电阻R2的电流是 。[1.5]
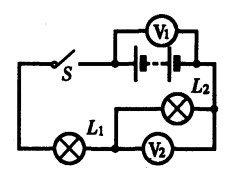
**23.如图15-8所示的电路,S合上后,电压表V1的示数是6V,V2的示数是3.8V,那么电灯L1两端的电压是 ,灯L2两端的电压是 。[1.5]
**24.一盏白炽灯接在家用电路上,灯泡正常发光时的电阻是1210Ω,求此灯正常发光时的电流是多大?[1.5]
25.加在某导体两端的电压为3V时,测出通过导体的电流是150mA,则该导体的电阻多大?
**26.用电压表测出一段导体两端的电压是72V,用电流表测出通过这段导体的电流为0.4A,则这段导体的电阻是 Ω。[1.0]
**27.一个电阻为5Ω的导体,通过它的电流为0.8A,说明它两端的电压是 V。[1.0]
**28.一个导体当它两端加8V电压时,通过它的电流为0.2A,则它的电阻是 Ω;这段导体两端加6V电压时,它的电流为 A,电阻为 Ω;当它两端不加电压时,导体的电阻是 Ω,通过导体的电流是 A。[3.0]
**29.有甲、乙两个导体,当通过相同的电流时,甲两端的电压比乙两端的电压高,则两者的电阻相比( )A.R甲>R乙 B.R甲=R乙 C.R甲<R乙 D.无法判定
**30.加在阻值12Ω的电阻两端的电压是6V,则在3分20秒内通过该电阻的电量是多少?
**31.某段电路两端的电压是220V,用电器的电阻是40Ω,能否用量程为0~3A的电流表测其电流?[1.5]
**32.加在阻值为30Ω的电阻两端的电压是6V,10min通过该电阻的电量是 C。[1.0]
**33.若导体两端加8V电压时,1min内通过导体横截面积的电量是18C,导体中的电流是 A,导体的电阻是 Ω;若导体两端不加电压时,导体的电阻为
Ω,通过导体的电流是 A。[2.5]
**34.甲、乙两个导体的电阻之比是1∶2,将它们分别接到同一电源的两端,则通过它们的电流之比是 。[1.0]
35.在电阻是5Ω的导体中,1.5min通过该导体的电量是45C,那么导体两端的电压是 V。
**36.一个5Ω的电阻两端电压为U时,通过电阻的电流为3A,如果将这个电压加在10Ω的电阻两端,则电流是 A。[1.0]
**37.当导体两端电压为10V时,通过导体的电流为500mA,那么导体两端电压为2V时,导体的电阻是( )。 A.0.004Ω B.0.02Ω C.4Ω D.20Ω
**38.在下面的方框内画出伏安法测电阻的电路图,并根据电路图连接15-9电路。[3.5]
在连接电路图时开关应处于 状态,滑动变阻器的滑片应位于 (填A或B)端,这主要是为了避免电路中的 过大,而烧坏电路中的有关元件。
**39.在伏安法测电阻的实验中,利用R=U/I计算出各次的电阻值。但算出的结果往往是不同的,这属于实验中的 ,是不可避免的,采取多次测量取平均值的办法可以 。[1.5]
**40.将6V的电压加在用电器两端时,通过的电流是0.2A,该用电器的电阻是
Ω;将3V的电压加在同一用电器两端时,通过电路的电流是 A,用电器的电阻是 Ω;如果用电器两端的电压为零,该电阻的阻值是 Ω。[2.0]
**41.如图15-10所示的电路,电源电压为6V,电灯L1上的电压为1.5V,则电压表的示数( )A.1.5V B.4.5V C.6V D.7.5V
***42.有甲、乙、丙三根用同种材料制成的导线,已知甲和乙粗细相同,但甲比乙长;乙和丙的长度相同,但乙比丙细。则三根导线中电阻最大的是( )。
[A.甲 B.乙 C.丙 D.无法判断
***43.质量相同的铜丝和铝丝,它们的横截面积相等,铜丝和铝丝的电阻相比较( )。
A.铜丝的电阻大 B.铝丝的电阻大
C.电阻一样大 D.无法比较
***44.如图15-11是滑动变阻器的结构示意图,若滑片向
右移动时,电路中的电流变小,则应选用的接线柱是( )。
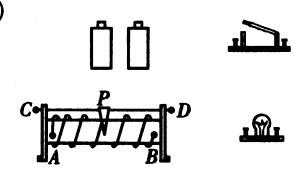
A.AC或AD B.BC或BD
C.AC或BD D.AB或BD
***45.请按要求将图15-12所示的器材用色笔连好电路并画出电路图。要求:当滑片向右移动时,电灯变亮。
知识的拓展
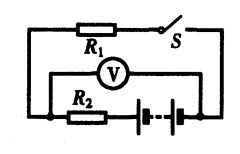
***46.下列说法中正确的是( )。[1.0]
A.电流表和电压表都可以直接接到电源的两极上
B.电流表可以直接接到电源的两极上,而电压表不行
C.电压表可以直接接到电源的两极上,而电流表不行
D.电流表和电压表都不能直接接到电源的两极上
***47.如图15-13闭合开关S,电压表测的电压是( )。[1.0]
A.R1两端的电压 B.R2两端的电压 C.R1和R2两端的电压 D.电源两端的电压
***48.一段导体两端的电压是2V时,导体中的电流是0.2A,如果电压增大到9V时,导体中的电流变为多大。[1.5]
***49.一只电阻器两端的电压从3V增加到3.8V时,通过该电阻器的电流增加了0.2A,则该电阻是多少?[1.5]
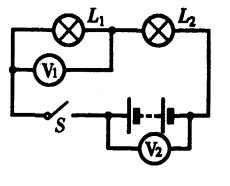
***50.在图15-14所示的电路中,当开关S闭合后,
电压表V1和V2示数相同,发生的故障是( )。[1.5]
A.灯L1的灯丝断了 B.灯L2的灯丝断了
C.开关S处断路 D.L1两接线柱短路
***51.当导体两端的电压是8V时,通过导体的电流是0.4A,如果使导体两端的电压再增加6V时,该导体中的电流是( )A.0.4A B.0.5A C.0.7A D.0.93A

***52.如图15-15所示,是滑动变阻器接入电路的4种情况,当变阻器的滑片向右移动时,使电路中电流增大的是( )。
***53.设计电路。要求:L1和L2串联,电流表测L1的电流,电压表测L2两端的电压,滑动变阻器控制电路中的电流不超过0.5A。画出电路图,并用铅笔线代替导线将图15-16中的元件连接起来。[3.5]
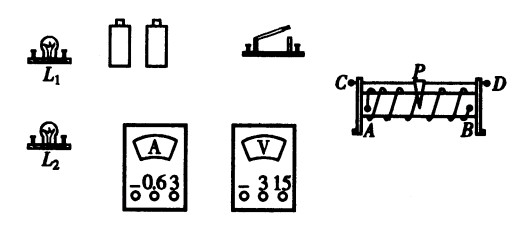
***54.加在导体两端的电压为3V,通过它的电流为200mA,如果将两端电压再增加6V时,应选什么量程的电流表测其电流?[1.5]
55.如图15-17所示的电路,灯L的电阻为10Ω,电源电压为6V,如果电压表被短路,那么( )A.电流表被烧坏 B.电压表被烧坏 C.灯L被烧坏 D.不发生任何事故
***56.某同学做伏安法测电阻的实验时,无论怎样移动变阻器的滑片,发现电压表的示数均为零,而电流表的指针指在满量程之外,这时( )。[1.5]
A.一定是电压表已损坏,应立即断开关
B.一定是电流表与电源两极直接相连,应立即断开开关
C.可能是电压表发生了故障,而电流表既未接错也未损坏
D.可能是电流表与电压表接成了串联电路
***57.如图15-18所示的电路中,电源电压不变,当开关闭合,滑动变阻器的滑片向左移动时( )A.电流表示数减小,电压表示数不变 B.电流表示数增大,电压表示数增大
C.电流表示数减小,电压表示数减小D.电流表示数增大,电压表示数减小
串联、并联电路的特点
基础知识与基本技能
*1.串联电路的总电阻等于 ,写成数学表达式是 ;串联电路中的电流 ,写成数学表达式是 ;串联电路的总电压等于 ,写成数学表达式是 。
*2.几个导体串联起来总电阻比其中任何一个导体的电阻都 ,因为导体的串联相当于增加了导体的 。[1.0]
**3.阻值为10Ω的电阻R1与阻值为25Ω的电阻R2串联后的总电阻是 。若通过R1的电流为0.2A,则通过电阻R2的电流是 ,R2两端的电压是 。[1.5]
**4.R1与R2串联后的总电阻为350Ω,已知电阻R1=170Ω,则电阻R2= Ω。
**5.电阻R1、R2串联在电路中,已知R1∶R2=3∶2,则通过的电流之比I1∶I2= ,电阻两端的电压之比U1∶U2= 。[2.5]
**6.R1=5Ω,R2=10Ω,串联后接到6V的电源上,则R1两端的电U1为 ,R2两端的电压U2为 ,U1∶U2= 。[2.5]
**7.电阻R1=30Ω,与电阻R2串联后总电阻为90Ω,则电阻R2为 Ω。将这两个电阻并联,其并联的电阻为 Ω。[1.5]
8.粗细相同的两根铝导线,长度关系是L1>L2,串联接入电路后,其电流和两端电压的关系是( )A.I1>I2,U1<U2 B.I1<I2,U1>U2 C.I1=I2,U1>U2 D.I1=I2,U1<U2
**9.串联电路随着用电器的个数增加,其总电阻( )。[1.0]
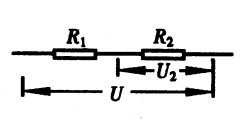
A.变大 B.变小 C.不变 D.无法判断
**10.已知:R1=4Ω,它与一只电阻R2并联后的总电阻是2.4Ω,求:R2的阻值。[1.5]
**11.如图15-19,R1=6Ω,U2=3V,总电压为7V,求:R2=?
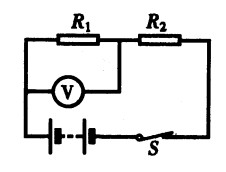
**12.如图15-20,R1=2Ω,R2=3Ω,电压表的示数为1V。求:R2两端的电压和电源电压。[1.5]
知识的应用
**13.在家庭电路中,同时工作的用电器越多,干路中的电流( )。[0.5]
A.越大 B.越小 C.不变 D.无法判断
**14.将电阻R1、R2并联在电路中,已知R1=4R2,则在通过R1、R2的电流之比为( )[1.5]
A.1:4 B.4:1 C.2:1 D.1:16
**15.将20只电阻都是9Ω的小灯泡串联后接在36V的电源上,通过其中一个小灯泡的电流为 mA。[1.0]
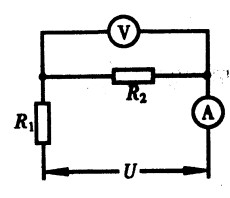
**16.如图15-21所示的电路,电压U为24V,电流表的示数为1.2A,电压表的示数为6V,则电阻R1阻值为 Ω。[1.0]
**17.电阻R1和R2串联后的总电阻是1.5kΩ,接入电路后,R1两端的电压为6V,R2两端的电压为3V,则R1的阻值是
Ω。[1.5]
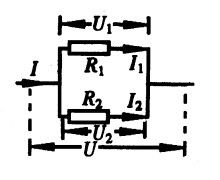
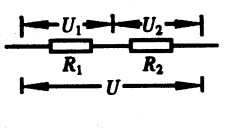
**18.如图15-22所示,已知R1=6Ω,U∶U2=4∶1,则R2的阻值是 Ω,U1∶U2= 。[2.0]
**19.把6个完全相同的小灯泡串联起来,接在24V的电路上,每个小灯泡两端的电压是 V。若每个小灯泡的电阻都是16Ω,电路中的电流是 A。[2.5]
**20.如图15-23所示的电路中,并联电路的电压U = ;干路中的电流I = ;总电阻的倒数1/R = 。[1.5]
**21.并联电路的总电阻比其中任何一个电阻都要 ,因为导体并联相当于 。[1.5]
**22.两个相同的电阻并联后的总电阻为4Ω,那么将它们串联后的总电阻是 Ω。[1.0]
**23.将6只30Ω的电阻并联起来,其电阻为 Ω,15Ω的电阻与30Ω的电阻并联,总电阻是 Ω。[1.5]
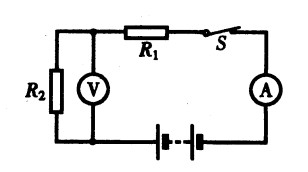
**24.将两个灯泡L1与L2并联,用电流表测出通过L1和干路中的电流分别为0.5A和0.7A,则通过L2的电流为 mA。[1.5]
25.将一阻值为10Ω的均匀的电阻丝对折后,当成一根使用,则对折后的电阻为 Ω。
***26.如图15-24所示的电路,R1的阻值为10Ω,电流表的示数为0.4A,电压表的示数为3.2V。求:R1两端的电压,R2的阻值及电源电压。[2.5]
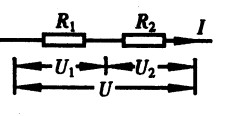
***27.如图15-25:U1=6V,U=10V,通过R1的电流是0.4A,求:R1、R2的阻值。[2.5]
***28.判断题:[2.5]
(1)( )导体的电阻决定于导体的长度、横截面积和材料,而与两端的电压和通过的电流无关
(2)( )欧姆定律公式中的I、U、R是同一电路上的电流、电压和电阻
(3)( )串联电路中的任一用电器被烧断时,其它用电器仍然正常工作
(4)( )串联电路上,其中一个电阻增大时,总电阻也增大
(5)( )金属中能够自由移动的是自由电子,所以电流和方向就是自由电子移动的方向
***29.两盏电灯L1、L2串联在家庭电路中,如果它们的电阻分别是440Ω和110Ω,求电路中的电流和电灯L1、L2两端的电压各多大?[2.5]
***30.R1与R2串联后,连到10V的电源上,R1=30Ω,测得R1两端的电压为6V,求:电路中的电流和R2的阻值。[2.5]
***31.R1、R2串联后接到18V的电源上,测得通过R1的电流为0.2A,R2的电阻是40Ω。求:R1的阻值和R2两端的电压。[2.5]
***32.R1=60Ω,R2=70Ω,它们串联后接到某电源上,测得5秒钟通过R1的电量是6C,则电源电压和R2两端的电压各多大?[2.5]

***33.如图15-26所示的电路,电源电压为20V,R1=25Ω,电流表的示数为0.25A,求R2的阻值和电压表的示数。[2.5]
***34.n个阻值分别为R1、R2……Rn电阻串联在电压为U的电路中,U1∶U2= ;U1∶U= ;Un∶U= 。由此可见串联电路中的总电压的分配与各部分电阻成 。[2.5]
***35.粗细相同的两根镍铬合金线A和B,A的长度大于B的长度,将它们串联后接入电路,则通过它们的电流和两端电压的关系是( )。[1.5]
A.IA>IB, UA=UB B. IA<IB, U1=U2 C.IA=IB, UA<UB D. IA=IB, UA>UB
***36.有三个电阻,阻值分别是3Ω、6Ω、9Ω,串联后接到6V的电源上,则三个电阻两端的电压分别是( )。
A.2V、4V、6V B.1V、2V、3V C.3V、2V、1V D.6V、4V、2V
***37.有一电铃正常工作的电压是12V,要将此电铃接到电压是20V的电源上,应如何办?
***38.一把电铬铁,正常工作的电阻是72Ω,通过的电流是0.1A,问必须给它串联一个多大的电阻才能把接到220V的电源上?[2.5]
***39.一个用电器正常工作的电压为6V,阻值为15Ω,将它与一只12Ω的电阻串联后接到电压是多大的电源上,此用电器才能正常工作?[2.5]
***40.两个电阻R1、R2,它们的阻值分别是10Ω、20Ω,将它们串联后接在电压为6V的电源上,通电5min,则通过R1、R2的电量分别是( )。[1.5]
A.1C,2C B.180C,90C C.40C,20C D.60C,60C
***41.将电阻R1、R2串联在电路中,已知:R1=3R2,总电压为4V,则R1两端的电压为( )。
A.4V B.3V C.2V D.1V
***42.两根长度相同,粗细不同的锰铜丝,把它们串联在电路中,则( )。[1.5]
A.粗的电流大,且电压也大 B.细的电流大,且电压也大
C.粗的、细的电流一样大,但细的电压大D.粗的、细的电流一样大,但粗的电压大
***43.一段导体的电阻增加3Ω后,接在原电源上,发现通过该导体的电流是原来的4/5,则该导体原来的阻值是多少?[2.5]
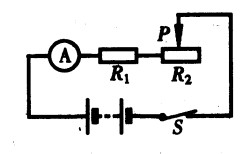
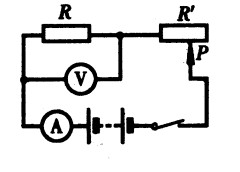
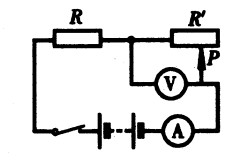
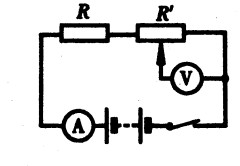
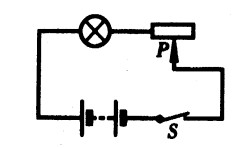
***44.如图15-27所示的电路,R1=20Ω,变阻器R2的阻值范围为0~40Ω,当变阻器滑片P移至变阻器的中点时,电流表的示数为0.5A,那么当变阻器滑片P移至阻值最大位置时,电流表的示数多大?[3.5]
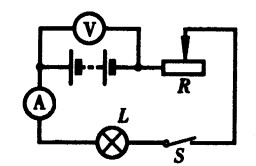
***45.如图15-28所示,小灯泡正常发光时灯丝的电阻是7.5Ω,电压是1.5V。如果电源电压为4V,要使小灯泡正常发光,应串联一个变阻器分去电压 V,并控制电路中的电流为 A,调节滑动变阻器的阻值为 Ω。[2.5]
***46.如图15-29所示,电流表的示数是0.3A,灯泡L的电阻为3Ω,整个电路的电阻为30Ω,那么,灯泡两端的电压为 V,电压表的示数是 V。
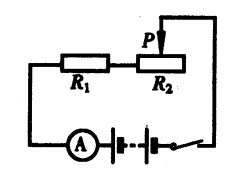
***47.如图15-30所示的电路中,当变阻器的滑片在向右移动过程中,变阻器连接入电路的阻值将 ,电路中的电流将 ,电阻R1两端的电压将 。(填“变大”、“变小”或“不变”)[2.5]
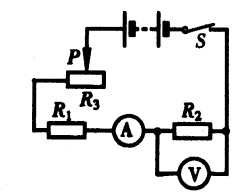
***48.如图15-31所示当滑动变阻器的滑片自左向右移动的过程中,电路的总电阻、电流表示数和电压表示数的变化情况分别是( )。[1.5]
A.变小、变大、不变 B.不变、变大、变小
C.变大、变小、变小 D.变大、变大、变大
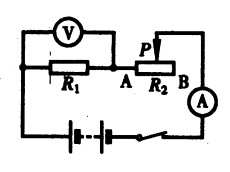
***49.如图15-32,R1=10Ω,R2是阻值为0~40Ω的变阻器,电源电压为10V。当P在B端时,电压表的示数多大?当P在AB中点时,电流表、电压表的示数各多大?[2.5]
***50.R1=5Ω,R2=7Ω,将R1、R2串联在某电路上,通过两电阻的电流之比I1∶I2= ,两电阻两端的电压之比U1∶U2= 。[2.0]
***51.下列各图15-33中,滑动变阻器滑片P移动时,电压表、电流表的示数各怎样变化:
若滑片P向右移动: 若滑片P向左移动: 若滑片P向右移动:
电流表示数 ; 电流表示数 ; 电流表示数 ;
电压表示数 ; 电压表示数 ; 电压表示数 ;
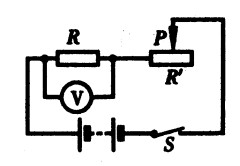
***52.如图15-34所示的电路,移动滑片P,使电压表的示数由U1变化到U2,U1∶U2=5∶2,则滑动变阻器滑片移动前后,通过电阻R的电流之比为( )。[2.5]
A.5∶2 B.2∶5 C.1∶1 D.无法判断
***53.将电阻R1和R2组成串联电阻,R1∶R2=3∶1,如果电路两端的总电压是12V,那么R1两端的电压是( )。[2.0]
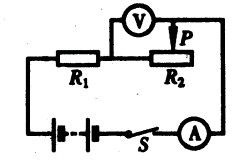
A.4V B.3V C.8V D.9V
***54.如图15-35所示的电路,电源电压为12V不变,R1=8Ω,R2是最大阻值为60Ω的变阻器。求电压表和电流表的变化范围。[2.5]
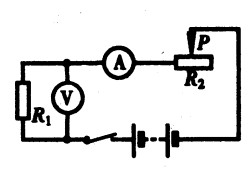
***55.如图15-36所示的电路,电源电压为12V且保持不变。R1=10Ω,R2是0~50Ω的变阻器。求当变阻器滑片移动时,电流表、电压表的示数变化范围。[2.5]
***56.某用电器R1上标有“10Ω 3A”,另一用电器R2上标有“50Ω 1.5A”,串联后接到电源上,为了使用电器正常工作,电源电压应不超过何值?[2.5]
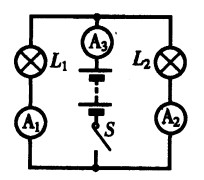
***57.如图15-37所示的电路,灯L1、L2是 联的,当开关S闭合后,电流表A1的示数为0.2A,A2的示数为A1示数的3倍,则A3的示数为 A。
***58.1Ω和10Ω的电阻并联后的总电阻是R1,1Ω、10Ω和100Ω的三电阻并联后的总电阻是R2,则R1、R2的大小关系是( )。
A.R1<R2 B.R1>R2 C.R1=R2 D.无法判断
***59.学校照明电路的总电阻( )。[1.5]
A.只开一盏灯时总电阻最小 B.不开灯时总电阻最小

C.所有灯都开着时总电阻最小 D.所有灯都开着时总电阻最大
60.如图15-38所示的电路,当滑动变阻器的滑片向右移动时,电流表、电压表的示数变化情况分别是( )A.变大,变大 B.变小,变小 C.变小,不变 D.变大,不变
***61.下面四对并联的电阻,总电阻最小的是( )。[1.5]
A.两个4Ω的 B.一个4Ω,一个6Ω
C.一个1Ω,一个8Ω D.一个2Ω,一个7Ω
***62.有一根粗细均匀的锰铜线,阻值为R,将其对折后的电阻是原电阻的( )。[1.5]
A.1/2倍 B.1/4倍 C.1/8倍 D.2倍
***63.两个电阻并联后的接入电路,总电阻为R,若将其中任一电阻的阻值减小,则总电阻将 R;若将其中任一个电阻的阻值增大,则总电阻将 R。(填“>,<或=”[1.5]
***64.两个同样的电阻串联后的总电阻是36Ω,若将它们并联后,总电阻是 Ω。
***65.导体串联后相当于增加了导体的 ,因此导体串联后总电阻 ;导体并联后相当于增加导体的 ,导体并联后总电阻 。[1.5]
***66.一根粗细均匀的电阻线,阻值为R,将其用拉丝机均匀拉长为原来的2倍,再将其对折,则它的电阻值 R。(填“>”,“<”或“=” [1.5]
***67.现有20Ω的电阻若干,实验时需要用5Ω的电阻一只,应用 只20Ω的电阻 联;若需要80Ω的电阻一只,应用 只20Ω的电阻 联。[1.5]
***68.现有阻值分别是2Ω,5Ω,8Ω和20Ω的电阻各一个,要获得4Ω的电阻可以将 的电阻 联;如果要获得10Ω的电阻,则应将 的电阻 联。[2.5]
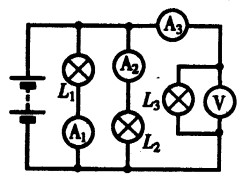
***69.如图15-39所示的电路中,电流表的读数:A1为0.12A,A2为0.08A,A3为0.1A,电压表的示数为2.8V。由此可知干路中的电流是 A;灯L1两端的电压为 V,灯L2两端的电压为 V。[2.5]
70.电阻R1=1Ω,R2=24Ω,把它们并联后的总电阻( )。A.一定大于24Ω, B.大于1Ω,小于24Ω
C.一定小于1Ω D.可能等于1Ω
***71.并联电路,随着并联支路数目增加,其总电阻将( )。[1.0]
A.变大 B.变小 C.不变 D.无法判断
***72.串联后的总电阻为10Ω的两个电阻,并联后可能的最大总电阻是( )。[2.5]
A.2.4Ω B.2.5Ω C.5Ω D.1.25Ω
***73.n个阻值相同的电阻,串联的总电阻与并联后的总电阻之比( )。[2.0]
A.n:1 B.n2:1 C.1:n D.1:n2
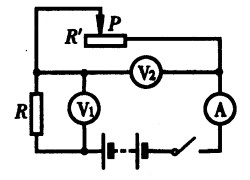
***74.如图15-40所示的电路,滑动变阻器的滑片P向右移动时,各电表示数变化情况是( )。[2.0]
A.V1增大,V2减小,A减小
B.V1增大,V2减小,A增大
C.V1减小,V2增大,A增大
D.V1减小,V2增大 A减小
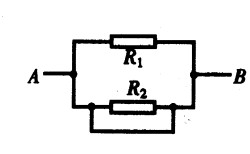
***75.如图15-41所示,R1=R2=10Ω,则A、B间的总电阻是( )。[1.0]
A.5Ω B.10Ω C.20Ω D.0Ω
***76.如图15-42,R1=5Ω,R2=20Ω,已知干路中的电流是0.5A,求电路两端的电压和通过的电阻的电流。[2.0]
***77.如图15-42,若电路两端的电压是9V,I=0.2A,I1=0.15A。求:R1、R2的阻值。[2.5]

***78.如图15-43,电源电压是18V,R1=60Ω,R2=10Ω,I1=0.2A。求:I2=?,I=?[2.5]
***79.一段电阻两端的电压是4V时,通过它的电流是0.2A,如果在它两端再并联上阻值为R的电阻时,干路中的电流增加了0.4A,那么电路的总电阻R总和R的阻值各是多大?[2.5]
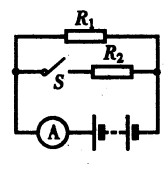
***80.如图15-44:R1=10Ω,R2=20Ω,S断开时,电流表的示数为0.6A.求S闭合时电流表的示数。[2.5]
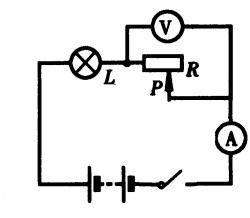
***81.如图15-45所示的电路,灯L的电阻RL=40Ω,R是标有“20Ω 1.5A”字样的变阻器,电源是由两节干电池串联而成的电池组。试求电流表和电压表的变化范围。[2.5]
***82.把R1与R2并联后接在电源上,当R1减小时,其总电阻( )。[1.0]
A.一定减小 B.一定增大 C.可能会增大 D.可能会减小
***83.把两根长度相同粗细不同的镍铬合金线连接在电路中,若通过它们的电流相等,则它们的连接方式是( )。[1.0]A.一定是串联 B.一定是并联
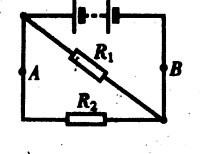
C.可能是串联,也可能是并联 D.无法判断
***84.如图15-46所示的电路,R1=2R2,电流表在A、B两处测得的电流分别为IA和IB,则( )。[2.5]
A.IA=![]() IB B.IA=
IB B.IA=![]() IB C.IA=
IB C.IA=![]() IB D.IA=IB
IB D.IA=IB
***85.将电阻R1、R2并联后接到某电源上,干路中的电流为I,则( )。[2.5]
A.R1中的电流为![]() B.电源电压为(
B.电源电压为(![]() )I
)I
C.R2上的电压为IR2 D.R1、R2上的电压之比为R2:R1
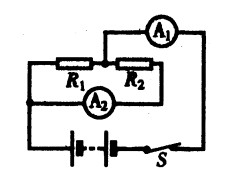
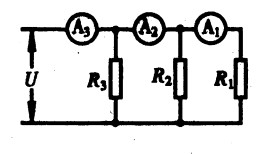
***86.如图15-47所示的电路,电流表A1与电流表A2的读数之比是5:2,则两个电阻R1与R2之比是( ) A.2:5 B.5:2 C.3:2 D.2:3
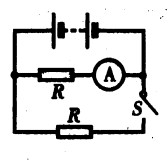
***87.如图15-48所示的电路,当开关S断开时,电流表的示数是1A,开关闭合时,电流表的示数将( )。A.不变 B.增加到2A C.减少到1/2A D.增加到4A
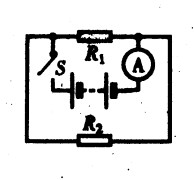
***88.如图15-49,电源电压4V,R1=R2=4Ω,R3=2Ω。电流表A1、A2、A3的示数分别是多少?[3.5]
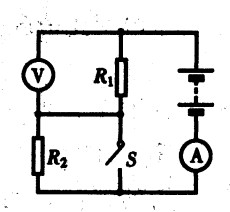
***89.如图15-50所示的电路,R1=2Ω,R2=6Ω,开关闭合后,电流表的示数为4.8A,求:[3.5]
(1)电路的总电阻;
(2)电阻R1、R2两端的电压之比;
(3)通过R1、R2的电流之比。
知识的拓展
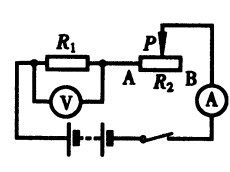
****90.如图15-51,当S闭合时,电流表的示数1.5A,电压表的示数为9V。(1)求电源电压和R1的阻值;(2)当S断开时,电压表的示数为6V,电流表的示数为1A,R2的阻值是多大?[3.5]
****91.如图15-52所示的电路,电源电压12V且保持不变。R1=8Ω,R2为0~12Ω的滑动变阻器。开关S合上后,变阻器滑片P从A端移动到B端时,求电流表、电压表的变化范围。
[3.5]
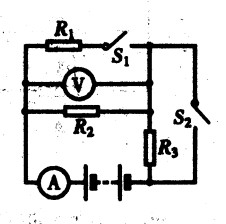
****92.如图15-53所示的电路,R1=9Ω,R2=6Ω,R3=4Ω。开关S1、S2均断开时,电压表的示数为5.4V。求:(1)开关S1、S2均闭合时,电流表、电压表的示数。(2)仅合上开关S2时,电压表、电压表的示数。[3.5]

****93.如图15-54所示的电路,灯L2的阻值R2=20Ω,当S1断开,S2合上时,电流表、电压表的示数分别为0.3A和3V。求:(1)电源电压;(2)S1、S2均合上时,电流表、电压表的示数。[3.5]
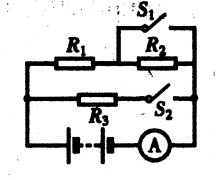
****94.如图15-55所示,R1=15Ω,R2=10Ω,当S1合上、S2断开时,电流表的示数为0.4A;当S1、S2均合上时,电流表的示数为0.6A。求:(1)R3的阻值;(2)S1、S2均断开时,电流表的示数。[3.5]

****95.如图15-56所示的电路,电源电压保持6V不变。灯L1的电阻为15Ω,当开关S1、S2闭合时,电流表的示数为1A,求灯L2的电阻。(2)当开关S1、S2都断开时,电流表的示数为0.3A,求L3的电阻。[3.5]
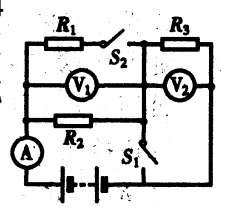
****96.如图15-57所示的电路,电源电压为12V且保持不变。R1=6Ω,R3=4Ω,当S1、S2均断开时,电流表的示数为1.2A。求:(1)R2的阻值;(2)当S1、S2均合上时,电流表和电压表的示数;(3)仅合上S1时,电流表、电压表的示数。[3.5]
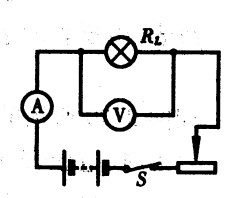
****97.如图15-58所示电路中,RL=6Ω,电流表的量程为0~0.6A,电压表的量程为0~3V,电源电压为8V。为了使两表都能安全使用,对变阻器连入电路的阻值有何要求?[3.5]

****98.如图15-59所示,R1为0~200Ω的变阻器,R2=50Ω,电源电压为20V,电流表的量程A1是0~0.6A,电流表A2的量程是0~3A。合上S,当滑动变阻器的滑片位于R1的中点时,1min通过R1的电量是多少?为了使两表都不损坏,R1连入电路的电阻只能在什么范围内变化?[4.5]
****99.实验:给你一个电池组,一只电压表,一只已知阻值的定值电阻R,一只开关和几根导线,请你用来测一个未知阻值的电阻RX。要求:(1)画出电路图;(2)简述实验原理和步骤;(3)写出计算RX的公式。[4.5]
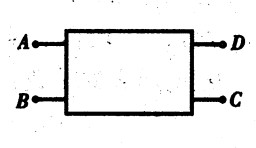
****100.如图15-60所示的方框称为黑箱(看不见内部情况的意思),它外面有四个接线柱,并知道内部有三只阻值相同的电阻,但不知道接法。经从外部对四接线柱进行测定,得知RAD=RBC=R,RAB=RCD=2R。请在黑箱内画出电阻的连接方法。[3.5]
检 测 题
(每题10分,共100分;完成时间30分钟)
基础知识与基本技能*1.电压是使电路中形成 的原因。电阻是表示导体对电流的 作用的,其它条件一定时,电阻越大,电流越小。
*2.在用实验研究一段导体(电阻)中的电流与它两端电压的关系时,应当运用滑动变阻器进行调节,不断地改变 值,并记录对应的 值,然后对数据进行分析得出结论;在研究一段导体(电阻)中的电流与导体电阻的关系时,每次实验应换用不同阻值的导体,并运用滑动变阻器进行调节,使每一次导体两端的电压 ,并记录对应的 值,然后对数据进行分析,得出结论。综合以上两方面的实验结果可得到著名的欧姆定律,其内容是 。
**3.一段导体两端的电压是6V时,通过导体的电流是200mA,则该导体的阻值为
Ω;若使该导体两端电压变为3V,则该导体的电阻为 Ω。
**4.已知两个导体的电阻分别为R1=4Ω,R2=6Ω。若将它们串联接人电路,则总电阻为 Ω,它们各自两端的电压U1∶U2= ;若将它们并联接人电路,则总电阻为 Ω,通过它们的电流之比I1∶I2= 。
知识的应用
**5.电阻R1:R2=4:3,它们并联后接入电路中,通过它们的电流之比为 ,它们两端的电压之比为 。
**6.在并联电路中,通过支路的电流跟该支路的电阻成 比,并联电路具有
作用。
***7.n个等值电阻并联后,总电阻R等于某一电阻的 倍,总电流等于某一条支路电流的 倍。
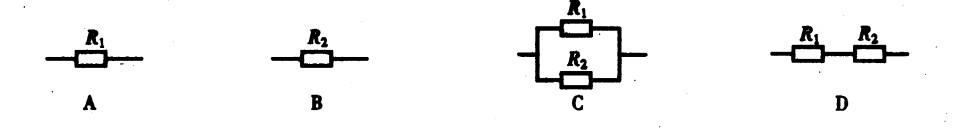
***8.已知:R1<R2,将图15-1中的四种不同接法接到同一电源的两极间,电路中的电流最小的是( )。
知识的拓展****9.给你一个电池组,一只电流表,一只已知阻值的定值电阻R,以及开关、导线。用这些器材测一个未知阻值的电阻Rx的阻值。要求:(1)画出电路图;(2)写出主要步骤和计算式。
****10.某同学用伏安法测一只小灯泡的电阻,请你回答该同学在实验中遇到的问题:
(1)灯泡的亮度在他看来是正常时,他停止了对滑动变阻器的调节,并细心地观察电流表,发现电流表的示数在缓慢地变小,你认为出现这种现象的原因是
。
(2)后来他又调节滑动变阻器,一不留神灯泡熄灭了(灯丝烧断了)。这时他观察到两电表的示数情况将是( )。
A.两电表示数都为零 B.电流表有示数,电压表示数为零
C.两电表的示数都不为零 D.电流表示数为零,电压表有示数且比原来大
人教版第十六章 热和能 复习提纲
一、分子热运动
1.物质是由分子组成的。分子若看成球型,其直径以10-10m来度量。
2.一切物体的分子都在不停地做无规则的运动。
①扩散:不同物质在相互接触时,彼此进入对方的现象。
②扩散现象说明:A、分子之间有间隙。B、分子在做不停的无规则的运动。
③课本中的装置下面放二氧化氮这样做的目的是:防止二氧化氮扩散被误认为是重力作用的结果。实验现象:两瓶气体混合在一起颜色变得均匀,结论:气体分子在不停地运动。
④固、液、气都可扩散,扩散速度与温度有关。
⑤分子运动与物体运动要区分开:扩散、蒸发等是分子运动的结果,而飞扬的灰尘,液、气体对流是物体运动的结果。
3.分子间有相互作用的引力和斥力。
①当分子间的距离d=分子间平衡距离r,引力=斥力。
②d<r时,引力<斥力,斥力起主要作用,固体和液体很难被压缩是因为:分子之间的斥力起主要作用。
③d>r时,引力>斥力,引力起主要作用。固体很难被拉断,钢笔写字,胶水粘东西都是因为分子之间引力起主要作用。
④当d>10r时,分子之间作用力十分微弱,可忽略不计。
破镜不能重圆的原因是:镜块间的距离远大于分子之间的作用力的作用范围,镜子不能因分子间作用力而结合在一起。
二、内能
1.内能:物体内部所有分子做无规则运动的动能和分子势能的总和,叫做物体的内能。
2.物体在任何情况下都有内能:既然物体内部分子永不停息地运动着和分子之间存在着相互作用,那么内能是无条件的存在着。无论是高温的铁水,还是寒冷的冰块。
3.影响物体内能大小的因素:①温度:在物体的质量,材料、状态相同时,温度越高物体内能越大;②质量:在物体的温度、材料、状态相同时,物体的质量越大,物体的内能越大;③材料:在温度、质量和状态相同时,物体的材料不同,物体的内能可能不同;④存在状态:在物体的温度、材料质量相同时,物体存在的状态不同时,物体的内能也可能不同。
4.内能与机械能不同:
机械能是宏观的,是物体作为一个整体运动所具有的能量,它的大小与机械运动有关。
内能是微观的,是物体内部所有分子做无规则运动的能的总和。内能大小与分子做无规则运动快慢及分子作用有关。这种无规则运动是分子在物体内的运动,而不是物体的整体运动。
5.热运动:物体内部大量分子的无规则运动叫做热运动。
温度越高扩散越快。温度越高,分子无规则运动的速度越大。
三、内能的改变
1.内能改变的外部表现:
物体温度升高(降低)──物体内能增大(减小)。
物体存在状态改变(熔化、汽化、升华)──内能改变。
反过来,不能说内能改变必然导致温度变化。(因为内能的变化有多种因素决定)
2.改变内能的方法:做功和热传递。
A、做功改变物体的内能:
①做功可以改变内能:对物体做功物体内能会增加。物体对外做功物体内能会减少。
②做功改变内能的实质是内能和其他形式的能的相互转化。
③如果仅通过做功改变内能,可以用做功多少度量内能的改变大小。(W=△E)
④解释事例:图15.2-5甲看到棉花燃烧起来了,这是因为活塞压缩空气做功,使空气内能增加,温度升高,达到棉花燃点使棉花燃烧。钻木取火:使木头相互摩擦,人对木头做功,使它的内能增加,温度升高,达到木头的燃点而燃烧。图15.2-5乙看到当塞子跳起来时,容器中出现了雾,这是因为瓶内空气推动瓶塞对瓶塞做功,内能减小,温度降低,使水蒸气液化凝成小水滴。
B、热传递可以改变物体的内能。
①热传递是热量从高温物体向低温物体或从同一物体的高温部分向低温部分传递的现象。
②热传递的条件是有温度差,传递方式是:传导、对流和辐射。热传递传递的是内能(热量),而不是温度。
③热传递过程中,物体吸热,温度升高,内能增加;放热温度降低,内能减少。
④热传递过程中,传递的能量的多少叫热量,热量的单位是焦耳。热传递的实质是内能的转移。
C、做功和热传递改变内能的区别:由于它们改变内能上产生的效果相同,所以说做功和热传递改变物体内能上是等效的。但做功和热传递改变内能的实质不同,前者能的形式发生了变化,后者能的形式不变。
D、温度、热量、内能的区别:
四、热量
1.比热容:⑴定义:单位质量的某种物质温度升高(降低)1℃时吸收(放出)的热量。
⑵物理意义:表示物体吸热或放热的本领的物理量。
⑶比热容是物质的一种特性,大小与物体的种类、状态有关,与质量、体积、温度、密度、吸热放热、形状等无关。
⑷水的比热容为4.2×103J(kg·℃)表示:1kg的水温度升高(降低)1℃吸收(放出)的热量为4.2×103J。
⑸水常调节气温、取暖、作冷却剂、散热,是因为水的比热容大。
2.计算公式:Q吸=Cm(t-t0),Q放=Cm(t0-t)。
3.热平衡方程:不计热损失Q吸=Q放。
五、内能的利用、热机
(一)内能的获得──燃料的燃烧
燃料燃烧:化学能转化为内能。
(二)热值
1.定义:1kg某种燃料完全燃烧放出的热量,叫做这种燃料的热值。
2.单位:J/kg。
3.关于热值的理解:
①对于热值的概念,要注重理解三个关键词“1kg”、“某种燃料”、“完全燃烧”。1kg是针对燃料的质量而言,如果燃料的质量不是1kg,那么该燃料完全燃烧放出的热量就不是热值。某种燃料:说明热值与燃料的种类有关。完全燃烧:表明要完全烧尽,否则1kg燃料化学能转变成内能就不是该热值所确定的值。
②热值反映的是某种物质的一种燃烧特性,同时反映出不同燃料燃烧过程中,化学能转变成内能的本领大小,也就是说,它是燃料本身的一种特性,只与燃料的种类有关,与燃料的形态、质量、体积等均无关。
3.公式:Q=mq(q为热值)。
实际中,常利用Q吸=Q放即cm(t-t0)=ηqm′联合解题。
4.酒精的热值是3.0×107J/kg,它表示:1kg酒精完全燃烧放出的热量是3.0×107J。
煤气的热值是3.9×107J/m3,它表示:1m3煤气完全燃烧放出的热量是3.9×107J。
5.火箭常用液态氢做燃料,是因为:液态氢的热值大,体积小便于储存和运输。
6.炉子的效率:
①定义:炉子有效利用的热量与燃料完全燃烧放出的热量之比。
②公式:η=Q有效/Q总=cm(t-t0)/qm′。
(三)内能的利用
1.内能的利用方式:
⑴利用内能来加热;从能的角度看,这是内能的转移过程。
⑵利用内能来做功;从能的角度看,这是内能转化为机械能。
2.热机:定义:利用燃料的燃烧来做功的装置。
能的转化:内能转化为机械能。
蒸气机──内燃机──喷气式发动机。
3.内燃机:将燃料燃烧移至机器内部燃烧,转化为内能且利用内能来做功的机器叫内燃机。它主要有汽油机和柴油机。
4.内燃机大概的工作过程:内燃机的每一个工作循环分为四个阶段:吸气冲程、压缩冲程、做功冲程、排气冲程。在这四个阶段,吸气冲程、压缩冲程和排气冲程是依靠飞轮的惯性来完成的,而做功冲程是内燃机中唯一对外做功的冲程,是由内能转化为机械能。另外压缩冲程将机械能转化为内能。
5.热机的效率:热机用来做有用功的那部分能量和完全燃烧放出的能量之比叫做热机的效率。
公式:η=W有用/Q总=W有用/qm。
提高热机效率的途径:使燃料充分燃烧;尽量减小各种热量损失;机件间保持良好的润滑、减小摩擦。
6.汽油机和柴油机的比较:
|
| 汽油机 | 柴油机 |
不 同 点 | 构造: | 顶部有一个火花塞 | 顶部有一个喷油嘴 |
吸气冲程 | 吸入汽油与空气的混合气体 | 吸入空气 | |
点燃方式 | 点燃式 | 压燃式 | |
效率 | 低 | 高 | |
应用 | 小型汽车、摩托车 | 载重汽车、大型拖拉机 | |
相同点 | 冲程:活塞在往复运动中从汽缸的一端运动到另一端。 一个工作循环活塞往复运动2次,曲轴和飞轮转动2周,经历四个冲程,做功1次。 | ||
六、能量守恒定律
1.自然界存在着多种形式的能量。尽管各种能量我们还没有系统地学习,但在日常生活中我们也有所了解,如跟电现象相联系的电能,跟光现象有关的光能,跟原子核的变化有关的核能,跟化学反应有关的化学能等。
2.在一定条件下,各种形式的能量可以相互转化和转移(列举学生所熟悉的事例,说明各种形式的能的转化和转移)。在热传递过程中,高温物体的内能转移到低温物体。运动的甲钢球碰击静止的乙钢球,甲球的机械能转移到乙球。在这种转移的过程中能量形式没有变。
3.在自然界中能量的转化也是普遍存在的。小朋友滑滑梯,由于摩擦而使机械能转化为内能;在气体膨胀做功的现象中,内能转化为机械能;在水力发电中,水的机械能转化为电能;在火力发电厂,燃料燃烧释放的化学能,转化成电能;在核电站,核能转化为电能;电流通过电热器时,电能转化为内能;电流通过电动机,电能转化为机械能。
4.能量守恒定律:能量既不会消灭,也不会创生,它只会从一种形式转化为其他形式,或者从一个物体转移到另一个物体,而在转化和转移的过程中,能量的总量保持不变。
能量的转化和守恒定律是自然界最普遍的、最重要的定律之一。
人教版第十六章 热和能 复习提纲
一、分子热运动
1.物质是由分子组成的。分子若看成球型,其直径以10-10m来度量。
2.一切物体的分子都在不停地做无规则的运动。
①扩散:不同物质在相互接触时,彼此进入对方的现象。
②扩散现象说明:A、分子之间有间隙。B、分子在做不停的无规则的运动。
③课本中的装置下面放二氧化氮这样做的目的是:防止二氧化氮扩散被误认为是重力作用的结果。实验现象:两瓶气体混合在一起颜色变得均匀,结论:气体分子在不停地运动。
④固、液、气都可扩散,扩散速度与温度有关。
⑤分子运动与物体运动要区分开:扩散、蒸发等是分子运动的结果,而飞扬的灰尘,液、气体对流是物体运动的结果。
3.分子间有相互作用的引力和斥力。
①当分子间的距离d=分子间平衡距离r,引力=斥力。
②d<r时,引力<斥力,斥力起主要作用,固体和液体很难被压缩是因为:分子之间的斥力起主要作用。
③d>r时,引力>斥力,引力起主要作用。固体很难被拉断,钢笔写字,胶水粘东西都是因为分子之间引力起主要作用。
④当d>10r时,分子之间作用力十分微弱,可忽略不计。
破镜不能重圆的原因是:镜块间的距离远大于分子之间的作用力的作用范围,镜子不能因分子间作用力而结合在一起。
二、内能
1.内能:物体内部所有分子做无规则运动的动能和分子势能的总和,叫做物体的内能。
2.物体在任何情况下都有内能:既然物体内部分子永不停息地运动着和分子之间存在着相互作用,那么内能是无条件的存在着。无论是高温的铁水,还是寒冷的冰块。
3.影响物体内能大小的因素:①温度:在物体的质量,材料、状态相同时,温度越高物体内能越大;②质量:在物体的温度、材料、状态相同时,物体的质量越大,物体的内能越大;③材料:在温度、质量和状态相同时,物体的材料不同,物体的内能可能不同;④存在状态:在物体的温度、材料质量相同时,物体存在的状态不同时,物体的内能也可能不同。
4.内能与机械能不同:
机械能是宏观的,是物体作为一个整体运动所具有的能量,它的大小与机械运动有关。
内能是微观的,是物体内部所有分子做无规则运动的能的总和。内能大小与分子做无规则运动快慢及分子作用有关。这种无规则运动是分子在物体内的运动,而不是物体的整体运动。
5.热运动:物体内部大量分子的无规则运动叫做热运动。
温度越高扩散越快。温度越高,分子无规则运动的速度越大。
三、内能的改变
1.内能改变的外部表现:
物体温度升高(降低)──物体内能增大(减小)。
物体存在状态改变(熔化、汽化、升华)──内能改变。
反过来,不能说内能改变必然导致温度变化。(因为内能的变化有多种因素决定)
2.改变内能的方法:做功和热传递。
A、做功改变物体的内能:
①做功可以改变内能:对物体做功物体内能会增加。物体对外做功物体内能会减少。
②做功改变内能的实质是内能和其他形式的能的相互转化。
③如果仅通过做功改变内能,可以用做功多少度量内能的改变大小。(W=△E)
④解释事例:图15.2-5甲看到棉花燃烧起来了,这是因为活塞压缩空气做功,使空气内能增加,温度升高,达到棉花燃点使棉花燃烧。钻木取火:使木头相互摩擦,人对木头做功,使它的内能增加,温度升高,达到木头的燃点而燃烧。图15.2-5乙看到当塞子跳起来时,容器中出现了雾,这是因为瓶内空气推动瓶塞对瓶塞做功,内能减小,温度降低,使水蒸气液化凝成小水滴。
B、热传递可以改变物体的内能。
①热传递是热量从高温物体向低温物体或从同一物体的高温部分向低温部分传递的现象。
②热传递的条件是有温度差,传递方式是:传导、对流和辐射。热传递传递的是内能(热量),而不是温度。
③热传递过程中,物体吸热,温度升高,内能增加;放热温度降低,内能减少。
④热传递过程中,传递的能量的多少叫热量,热量的单位是焦耳。热传递的实质是内能的转移。
C、做功和热传递改变内能的区别:由于它们改变内能上产生的效果相同,所以说做功和热传递改变物体内能上是等效的。但做功和热传递改变内能的实质不同,前者能的形式发生了变化,后者能的形式不变。
D、温度、热量、内能的区别:
四、热量
1.比热容:⑴定义:单位质量的某种物质温度升高(降低)1℃时吸收(放出)的热量。
⑵物理意义:表示物体吸热或放热的本领的物理量。
⑶比热容是物质的一种特性,大小与物体的种类、状态有关,与质量、体积、温度、密度、吸热放热、形状等无关。
⑷水的比热容为4.2×103J(kg·℃)表示:1kg的水温度升高(降低)1℃吸收(放出)的热量为4.2×103J。
⑸水常调节气温、取暖、作冷却剂、散热,是因为水的比热容大。
2.计算公式:Q吸=Cm(t-t0),Q放=Cm(t0-t)。
3.热平衡方程:不计热损失Q吸=Q放。
五、内能的利用、热机
(一)内能的获得──燃料的燃烧
燃料燃烧:化学能转化为内能。
(二)热值
1.定义:1kg某种燃料完全燃烧放出的热量,叫做这种燃料的热值。
2.单位:J/kg。
3.关于热值的理解:
①对于热值的概念,要注重理解三个关键词“1kg”、“某种燃料”、“完全燃烧”。1kg是针对燃料的质量而言,如果燃料的质量不是1kg,那么该燃料完全燃烧放出的热量就不是热值。某种燃料:说明热值与燃料的种类有关。完全燃烧:表明要完全烧尽,否则1kg燃料化学能转变成内能就不是该热值所确定的值。
②热值反映的是某种物质的一种燃烧特性,同时反映出不同燃料燃烧过程中,化学能转变成内能的本领大小,也就是说,它是燃料本身的一种特性,只与燃料的种类有关,与燃料的形态、质量、体积等均无关。
3.公式:Q=mq(q为热值)。
实际中,常利用Q吸=Q放即cm(t-t0)=ηqm′联合解题。
4.酒精的热值是3.0×107J/kg,它表示:1kg酒精完全燃烧放出的热量是3.0×107J。
煤气的热值是3.9×107J/m3,它表示:1m3煤气完全燃烧放出的热量是3.9×107J。
5.火箭常用液态氢做燃料,是因为:液态氢的热值大,体积小便于储存和运输。
6.炉子的效率:
①定义:炉子有效利用的热量与燃料完全燃烧放出的热量之比。
②公式:η=Q有效/Q总=cm(t-t0)/qm′。
(三)内能的利用
1.内能的利用方式:
⑴利用内能来加热;从能的角度看,这是内能的转移过程。
⑵利用内能来做功;从能的角度看,这是内能转化为机械能。
2.热机:定义:利用燃料的燃烧来做功的装置。
能的转化:内能转化为机械能。
蒸气机──内燃机──喷气式发动机。
3.内燃机:将燃料燃烧移至机器内部燃烧,转化为内能且利用内能来做功的机器叫内燃机。它主要有汽油机和柴油机。
4.内燃机大概的工作过程:内燃机的每一个工作循环分为四个阶段:吸气冲程、压缩冲程、做功冲程、排气冲程。在这四个阶段,吸气冲程、压缩冲程和排气冲程是依靠飞轮的惯性来完成的,而做功冲程是内燃机中唯一对外做功的冲程,是由内能转化为机械能。另外压缩冲程将机械能转化为内能。
5.热机的效率:热机用来做有用功的那部分能量和完全燃烧放出的能量之比叫做热机的效率。
公式:η=W有用/Q总=W有用/qm。
提高热机效率的途径:使燃料充分燃烧;尽量减小各种热量损失;机件间保持良好的润滑、减小摩擦。
6.汽油机和柴油机的比较:
|
| 汽油机 | 柴油机 |
不 同 点 | 构造: | 顶部有一个火花塞 | 顶部有一个喷油嘴 |
吸气冲程 | 吸入汽油与空气的混合气体 | 吸入空气 | |
点燃方式 | 点燃式 | 压燃式 | |
效率 | 低 | 高 | |
应用 | 小型汽车、摩托车 | 载重汽车、大型拖拉机 | |
相同点 | 冲程:活塞在往复运动中从汽缸的一端运动到另一端。 一个工作循环活塞往复运动2次,曲轴和飞轮转动2周,经历四个冲程,做功1次。 | ||
六、能量守恒定律
1.自然界存在着多种形式的能量。尽管各种能量我们还没有系统地学习,但在日常生活中我们也有所了解,如跟电现象相联系的电能,跟光现象有关的光能,跟原子核的变化有关的核能,跟化学反应有关的化学能等。
2.在一定条件下,各种形式的能量可以相互转化和转移(列举学生所熟悉的事例,说明各种形式的能的转化和转移)。在热传递过程中,高温物体的内能转移到低温物体。运动的甲钢球碰击静止的乙钢球,甲球的机械能转移到乙球。在这种转移的过程中能量形式没有变。
3.在自然界中能量的转化也是普遍存在的。小朋友滑滑梯,由于摩擦而使机械能转化为内能;在气体膨胀做功的现象中,内能转化为机械能;在水力发电中,水的机械能转化为电能;在火力发电厂,燃料燃烧释放的化学能,转化成电能;在核电站,核能转化为电能;电流通过电热器时,电能转化为内能;电流通过电动机,电能转化为机械能。
4.能量守恒定律:能量既不会消灭,也不会创生,它只会从一种形式转化为其他形式,或者从一个物体转移到另一个物体,而在转化和转移的过程中,能量的总量保持不变。
能量的转化和守恒定律是自然界最普遍的、最重要的定律之一。
 阅读信息,回答问题
阅读信息,回答问题