题目内容
用一根细线把小钢球悬挂起来,这叫做单摆,是最简单的振动系统,如图所示,将小球稍微推离平衡位置到达a,然后放手,它就开始摆动,假如没有空气阻力,小球将一直摆动下去,永不停止。仔细观察摆动过程,可以发现小球来回摆动一周所需的时间总是一样的,这就是单摆的等时性,这个时间称为振动的周期。小明猜想单摆振动周期的大小可能与单摆的摆长L、偏离中心夹角θ及摆球质量有关,于是小明做了分别改变单摆的摆长、偏离中心夹角、摆球质量的摆动实验,并测出了各种情形下的单摆周期,如表1、2、3所示。




(1)通过对实验数据的分析,可得出什么结论?
___________________________________________________________________________________。
(2)单摆的等时性在什么地方有应用?
___________________________________________________________________________________。
(3)机械摆钟走得太快,应怎样调节摆长?
___________________________________________________________________________________。
___________________________________________________________________________________。
(2)单摆的等时性在什么地方有应用?
___________________________________________________________________________________。
(3)机械摆钟走得太快,应怎样调节摆长?
___________________________________________________________________________________。
(1)单摆的周期只与摆长有关,摆长越长,周期越大。 (或单摆的周期与摆动的幅度无关;或单摆的周期与摆球的质量无关);(合理即可)
(2)机械摆钟(或挂钟);(答案不唯一)
(3)应把摆长调节长些。
(2)机械摆钟(或挂钟);(答案不唯一)
(3)应把摆长调节长些。

练习册系列答案
相关题目
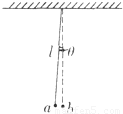
用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.
表一 m=10g θ=4°
表二 m=10g l=1m
表三 θ=4° l=1m
(1)根据以上实验数据.分折得出的结论是 .
(2)单摆的等时性主要应用在 上.
(3)机械摆钟走时太快,应将摆长 .
表一 m=10g θ=4°
| 摆长/m | 0.5 | 1 | 1.5 | 2 |
| 周期/s | 1.4 | 2 | 2.4 | 2.8 |
| 摆角θ | 1° | 2° | 3° | 4° |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆球质量/g | 5 | 10 | 15 | 20 |
| 周期/s | 2 | 2 | 2 | 2 |
(2)单摆的等时性主要应用在 上.
(3)机械摆钟走时太快,应将摆长 .



 用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.
用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.
