题目内容
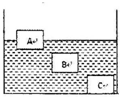 如图所示,A、B、C三个体积相同的立方体,静止在同种液体中.下列说法正确的是
如图所示,A、B、C三个体积相同的立方体,静止在同种液体中.下列说法正确的是
- A.把A、B立方体捆绑在一起,一定漂浮在该液面上
- B.把B、C立方体捆绑在一起,可能漂浮在该液面上
- C.把A、C立方体捆绑在一起,一定漂浮在该液面上
- D.把A、C立方体捆绑在一起,一定沉在容器底部
A
分析:因为A、B、C为体积相同的三个立方体,则体积相同,都放在同一液体中,所受浮力看排开液体的体积,排开体积大的所受浮力大,再根据物体所处的状态得出每个物体所受的浮力和各自的重力关系,最后比较立方体捆绑在一起时所受浮力和重力的大小即可判断.
解答:∵A漂浮,B悬浮,C下沉.则GA=F浮A=ρg×V排<ρgV物,GB=F浮B=ρgV物,GC>F浮C=ρgV物,
∵A、B、C三个体积相同的立方体,根据阿基米德原理和图中的物体排开液体的体积大小可得:
F浮A<F浮B=F浮C,
∴GA<GB<GC,
①把A、B立方体捆绑在一起,重力为GAB=GA+GB<ρgV物+ρgV物=2ρgV物,若全部浸没时,F浮AB=2ρgV物,所以
F浮AB>GAB,物体会上浮,最后漂浮,故A选项正确.
②把B、C立方体捆绑在一起,重力为GBC=GB+GC>ρgV物+ρgV物=ρgV物,若全部浸没时,F浮BC=2ρgV物,所以
GBC>F浮BC,物体会下沉,故B选项错误.
③把A、C立方体捆绑在一起,重力为GAC=GA+GC,若全部浸没时,F浮AC=2ρgV物,
∵GA<ρgV物,GC>ρgV物,∴GAC与2ρgV物无法比较大小,
由此可知,F浮AC与GAB的大小无法判断,所以物体状态不能判断,故C、D选项错误.
故选A.
点评:本题考查阿基米德原理的应用,关键是线判断出各物体的重力和所受浮力的大小,然后判断物体捆绑在一起时所受浮力和重力的大小关系.
分析:因为A、B、C为体积相同的三个立方体,则体积相同,都放在同一液体中,所受浮力看排开液体的体积,排开体积大的所受浮力大,再根据物体所处的状态得出每个物体所受的浮力和各自的重力关系,最后比较立方体捆绑在一起时所受浮力和重力的大小即可判断.
解答:∵A漂浮,B悬浮,C下沉.则GA=F浮A=ρg×V排<ρgV物,GB=F浮B=ρgV物,GC>F浮C=ρgV物,
∵A、B、C三个体积相同的立方体,根据阿基米德原理和图中的物体排开液体的体积大小可得:
F浮A<F浮B=F浮C,
∴GA<GB<GC,
①把A、B立方体捆绑在一起,重力为GAB=GA+GB<ρgV物+ρgV物=2ρgV物,若全部浸没时,F浮AB=2ρgV物,所以
F浮AB>GAB,物体会上浮,最后漂浮,故A选项正确.
②把B、C立方体捆绑在一起,重力为GBC=GB+GC>ρgV物+ρgV物=ρgV物,若全部浸没时,F浮BC=2ρgV物,所以
GBC>F浮BC,物体会下沉,故B选项错误.
③把A、C立方体捆绑在一起,重力为GAC=GA+GC,若全部浸没时,F浮AC=2ρgV物,
∵GA<ρgV物,GC>ρgV物,∴GAC与2ρgV物无法比较大小,
由此可知,F浮AC与GAB的大小无法判断,所以物体状态不能判断,故C、D选项错误.
故选A.
点评:本题考查阿基米德原理的应用,关键是线判断出各物体的重力和所受浮力的大小,然后判断物体捆绑在一起时所受浮力和重力的大小关系.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
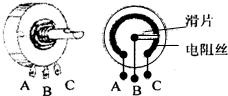 12、在收音机等电器中,有一种叫电位器的变阻器.电位器的外形及其内部构造如图所示.A、B、C三个焊接点相当于变阻器的三个接线柱.使用电位器时,下列说法中不正确的是( )
12、在收音机等电器中,有一种叫电位器的变阻器.电位器的外形及其内部构造如图所示.A、B、C三个焊接点相当于变阻器的三个接线柱.使用电位器时,下列说法中不正确的是( )
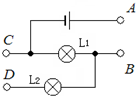 如图所示,A、B、C、D表示四个接线柱,请按下述要求,用导线将有关接线柱连接起来.要使L1发光,L2不亮,则连接
如图所示,A、B、C、D表示四个接线柱,请按下述要求,用导线将有关接线柱连接起来.要使L1发光,L2不亮,则连接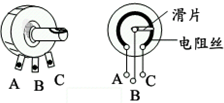 在收音机等电器中,有一种叫做电位器的元件.电位器的外形及内部构造如图所示.A、B、C三个焊接点相当于滑动变阻器的三个接线柱.以下说法正确的是.
在收音机等电器中,有一种叫做电位器的元件.电位器的外形及内部构造如图所示.A、B、C三个焊接点相当于滑动变阻器的三个接线柱.以下说法正确的是.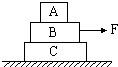 如图所示,A、B、C三物体叠放在水平桌面上,现用F=15N的拉力使三物体一起向右做匀速直线运动,则物体A受
如图所示,A、B、C三物体叠放在水平桌面上,现用F=15N的拉力使三物体一起向右做匀速直线运动,则物体A受