题目内容
 (2013?广东)如图是某装置利用浮力进行自动控制的原理图AOB为一杠杆(质量忽略不计),OA:OB=1:2. A端用细线挂一空心铝球,质量为2.7kg. 当铝球一半体积浸在水中,在B端施加3.5N的竖直向下的拉力F时,杠杆恰好在水平位置平衡.则铝球实心部分的体积为
(2013?广东)如图是某装置利用浮力进行自动控制的原理图AOB为一杠杆(质量忽略不计),OA:OB=1:2. A端用细线挂一空心铝球,质量为2.7kg. 当铝球一半体积浸在水中,在B端施加3.5N的竖直向下的拉力F时,杠杆恰好在水平位置平衡.则铝球实心部分的体积为10-3
10-3
m3,铝球受到的浮力为20
20
N.(ρ铝=2.7×103kg/m3,g=10N/kg)分析:已知铝球的质量和密度,根据密度公式可求出铝球实心部分的体积;对铝球进行受力分析可知,铝球受到细线的拉力、重力和浮力作用,因此杠杆A端受到竖直向下的拉力等于G-F浮,根据杠杆平衡的条件可求出浮力.
解答:解:∵ρ=
,
∴铝球实心部分的体积:V=
=
=10-3m3;
由杠杆平衡的条件可得:
(G-F浮)×OA=FB×OB
(2.7kg×10N/kg-F浮)×OA=3.5N×OB
2.7kg×10N/kg-F浮=7N
F浮=20N.
故答案为:10-3;20.
| m |
| v |
∴铝球实心部分的体积:V=
| m |
| ρ |
| 2.7kg |
| 2.7×103kg/m3 |
由杠杆平衡的条件可得:
(G-F浮)×OA=FB×OB
(2.7kg×10N/kg-F浮)×OA=3.5N×OB
2.7kg×10N/kg-F浮=7N
F浮=20N.
故答案为:10-3;20.
点评:本题考查了学生对密度公式和杠杆平衡条件的掌握和运用,关键是分析出作用在杠杆A端的力,难度不大.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
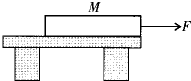 (2013?广东)如图所示,水平桌面上有一长为L,质量分布均匀的木板M,右端与桌边相齐,在水平力F的作用下,沿直线向右匀速离开桌边,在此过程中,下列说法正确的是( )
(2013?广东)如图所示,水平桌面上有一长为L,质量分布均匀的木板M,右端与桌边相齐,在水平力F的作用下,沿直线向右匀速离开桌边,在此过程中,下列说法正确的是( ) (2013?广东)如题图甲是探究“平面镜成像特点”的实验.
(2013?广东)如题图甲是探究“平面镜成像特点”的实验.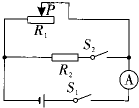 (2013?广东)如图所示的电路,电源电压为6V且保持不变,滑动变阻器R 标有“50Ω,2A”字样.
(2013?广东)如图所示的电路,电源电压为6V且保持不变,滑动变阻器R 标有“50Ω,2A”字样.