��Ŀ����
һ����Ȳ��Ƶ�Բ����ˮͰ�������Ϊ4��10��2m2��ʢ��һЩˮ���ˮƽ�����ѹ��Ϊ400N����gȡ10N/kg����
��1����ʱˮͰ�Ե����ѹǿΪ���
��2��Ͱ�IJ������һ��С����A�����ܳ��ܵ�ˮ��ѹǿ���Ϊ6��103Pa����A��ˮ�����ʱ��������ˮ�忪��
��3�����ڣ���֪С����A��ˮ��0.5m����ͼ������һ�����Ϊ5��10��3m3��ʵ�ĸ������ˮ�У��պ��ܹ���A�忪��������ܶ�Ϊ���٣�
��1��ˮͰ�Ե����ѹǿΪ1��104Pa��
��2��Ͱ��A��ˮ��0.6mʱ��������ˮ�忪��
��3��������ܶ�Ϊ0.8��103kg/m3��
���������������1��֪��ѹ�������������С������ѹǿ��ʽ��Ͱ�Ե����ѹǿ��
��2��֪������A�ܳ��ܵ�ˮ�����ѹǿ������Һ��ѹǿ��ʽp=��gh�����Aˮ�
��3����һ������Ž�ˮ�кպð�A�忪��˵��ˮ����������0.6m������ˮ�������ֵ��֪��������������������ſ�ˮ����������ð�����ԭ�������ܵ��ĸ������Ƚ��ſ�ˮ���������������С��ϵ�ó�����ˮ��������״̬��Ư���������������Ư������������ء�����������������ܶȹ�ʽ������ܶȣ�
��1��p==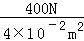 =1��104Pa��
=1��104Pa��
��2����p=��gh=6��103Pa��
��h=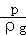 =
=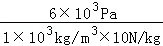 =0.6m��
=0.6m��
��3����һ������Ž�ˮ�кպð�A�忪��˵��ˮ����������0.6m�����h=0.1m��
V��=S��h=4��10��2m2��0.1m=4��10��3m3��
F��=��ˮV��g=1��103kg/m3��4��10��3m3��10N/kg=40N��
��V��=4��10��3m3��5��10��3m3��
������ˮ���ϣ�
��G=F��=40N��
���������
m==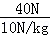 =4kg��
=4kg��
����ܶȣ�
��==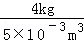 =0.8��103kg/m3��
=0.8��103kg/m3��
���㣺ѹǿ�Ĵ�С������㣻�ܶȹ�ʽ��Ӧ�ã������ļ��㣻Һ���ѹǿ�ļ��㣻������ԭ��������ĸ�����������Ӧ�ã�
����������Ϊ��ѧ�ۺ��⣬������ѧ�����ܶȹ�ʽ��������ʽ��Һ��ѹǿ��ʽ��ѹǿ��ʽ��������ԭ���������Ư�����������պ����ã�Ҫ�����ѡ�ù�ʽ���㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ϊ8kg�ľ���ľ�飬��������ĽӴ����Ϊ100cm2������2N����ʹ����ˮƽ����������ǰ��1m����ͼ����������������ǣ�������
| A��ľ��������֮��Ħ������С��2N |
| B��ľ�����˶������л�е�ܲ��� |
| C��ľ��������ѹǿ��800Pa |
| D�������ڴ˹�����������2J |
ѧϰ��ͬһֱ�ߵĶ����ĺϳ�֪ʶ��С������������������ϵĶ�������ͬһֱ���ϣ����ǻ���һ���ļнǣ���ô����F�Ĵ�С����������F1��F2�Ĵ�С���Ƿ���F����F1��F2�Ĺ�ϵ�أ�������Ӧ�ý̲���ѧ���ķ������Դ˽�����̽��.
��1������ͼ��ʾ����Ƥ��ԭ��ΪAB��ͨ���������ɲ����ƶ���Ƥ��ʩ�ӻ���һ���нǵ�������F1��F2��ʹ��Ƥ���쳤��C����¼��ʱF1��F2�Ĵ�С����ȥ��F1��F2����һ�����ɲ����ƶ���Ƥ��ʩ��һ����F�����ã�Ϊ��ʹ�����F������Ч������������F1��F2������Ч�� ��Ӧʹ��Ƥ�� ����¼��ʱF�Ĵ�С.
��2���Ⱥ����θı�F1��F2�ļнǣ��ظ����裨1�����õ�����ʵ���������±���ʾ��
| ������ ʵ����� | F1/N | F2/N | F1��F2�ļн� | ����F/N |
| 1 | 4 | 5 | ��1 | 8.7 |
| 2 | 4 | 5 | ��2 | 8.3 |
| 3 | 4 | 5 | ��3 | 7.8 |
| ��ע����1<��2<��3 | ||||
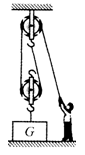

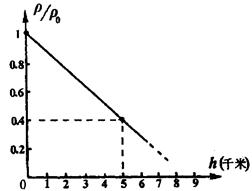
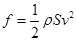 �����Ц�Ϊ�����ܶȣ�SΪɳ�������ĺ�������vΪ���٣����ɳ�����ܶȦ�ɳΪ3��103kg/m3��ɳ���뾶rΪ2.5��10-4m������Ŀ����ܶȦ�0Ϊ1.25 kg/m3����ôҪ�γ�ɳ����������ķ�������Ϊ_________m/s����������ܶȦ������߶�h�ı仯��ϵ��ͼ��ʾ����ô���������Ϊ8m/sʱ������ɳ���������߶�Ϊ_________m����gȡ10N/kg��ɳ���ɽ��ƿ������壬�����
�����Ц�Ϊ�����ܶȣ�SΪɳ�������ĺ�������vΪ���٣����ɳ�����ܶȦ�ɳΪ3��103kg/m3��ɳ���뾶rΪ2.5��10-4m������Ŀ����ܶȦ�0Ϊ1.25 kg/m3����ôҪ�γ�ɳ����������ķ�������Ϊ_________m/s����������ܶȦ������߶�h�ı仯��ϵ��ͼ��ʾ����ô���������Ϊ8m/sʱ������ɳ���������߶�Ϊ_________m����gȡ10N/kg��ɳ���ɽ��ƿ������壬�����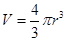 )
)