题目内容
【题目】如图甲所示，一个柱形容器放在水平桌面上，容器中立放着一个底面积为100cm2 ， 高为12cm均匀实心长方体木块A，A的底部与容器底用一根细绳连在一起，现慢慢向容器中加水，当加入1.8kg的水时，木块A对容器底部的压力刚好为0，如图乙所示，此时容器中的水的深度为9cm．已知细绳长度为L=8cm，ρ水=1.0×103kg/m3 ． 求：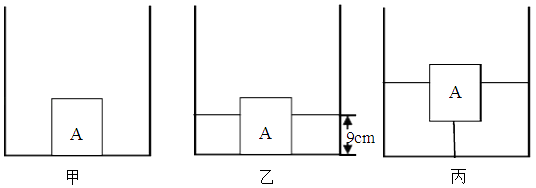 
（1）当木块A对容器底部的压力刚好为0，A受到的浮力；
（2）木块A的密度；
（3）若继续缓慢向容器中加水，当容器中的水的总质量为4.5kg时，停止加水，如图丙所示，此时将与A相连的细绳剪断，求细绳剪断前、剪断后木块静止时，水对容器底部压强的变化量．（整个过程中无水溢出）
【答案】
（1）解：已知木块A的底面积S木=100cm2，
由乙图可知：当木块A对容器底部的压力刚好为0，水的深度为h水=9cm；
则木块A排开水的体积：V排=S木h水=100cm2×9cm=900m3=9×10﹣4m3，
木块受到的浮力：
F浮=ρ水V排g=1×103kg/m3×9×10﹣4m3×10N/kg=9N
（2）解：木块A的体积：V木=S木h木=100cm2×12cm=1200cm3=1.2×10﹣3m3，
由于木块A对容器底部的压力刚好为0，木块A处于漂浮，则G=F浮=9N，
由G=mg=ρVg可得木块的密度：
ρ木= 
= 
=0.75×103kg/m3
（3）解：木块A对容器底部的压力刚好为0时，由ρ= 
可得所加水的体积为：
V水1= 
= 
=1.8×10﹣3m3=1800cm3；
由乙图可知：V水1=（S容﹣S木）h水，（其中h水=9cm）
则容器的底面积为：
S容= 
+S木= 
+100cm2=300cm2；
再次加水后容器中水的总体积为：
V水2= 
= 
=4.5×10﹣3m3=4500cm3；
如上图丙中可知，木块下表面以下水的体积（图中红线以下）为：
V1=S容L=300cm2×8cm=2400cm3，
则红线以上水的体积为：
V2=V水2﹣V1=4500cm3﹣2400cm3=2100cm3，
设此时木块浸入水的深度为h′，则V2=（S容﹣S木）h′，
所以，木块浸入水的深度：h′= 
= 
=10.5cm，
此时木块排开水的体积为V排′=S木h′=100cm2×10.5cm=1050cm3；
若将细线剪断，木块将上浮，当木块静止时漂浮如上图丁，
由于图丁与图甲中的木块都是漂浮，则木块受到的浮力相等，排开水的体积相等，
所以，细线剪断后木块漂浮时，其排开水的体积为V排″=V排=900cm3，
细绳剪断前、剪断后，排开水的体积变化量：△V排=V排′﹣V排″=1050cm3﹣900cm3=150cm3，
则水的深度变化量：
△h═ 
= 
=0.5cm=5×10﹣3m，
所以，水对容器底部压强的变化量：△p=ρ水g△h=1×103kg/m3×10N/kg×5×10﹣3m=50Pa．
【解析】（1）根据木块A底面积和水的深度，可求木块A排开水的体积，再利用阿基米德原理求物块受到的浮力；（2）由于木块A对容器底部的压力刚好为0，则重力与浮力相等；利用G=mg求木块的质量，再利用密度公式求木块的密度；（3）根据水的体积求出木块A浸入水的体积，进一步求细绳剪断前、剪断后排开水的体积变化，知道容器底面积，可求水深的变化量，再利用液体压强公式求容器底所受压强改变量．
【考点精析】本题主要考查了阿基米德原理和物体的浮沉条件及其应用的相关知识点，需要掌握阿基米德原理：浸在液体中的物体受到向上的浮力，浮力的大小等于物体排开的液体所受的重力．这个规律叫做阿基米德原理，即 F浮= G排 =ρ液gv排；物体的浮沉条件：浸没在液体中的物体 F浮＞G 时上浮，F浮 = G 时悬浮，F浮 ＜G 时下沉．物体浮沉条件的应用举例：（1）轮船（2）潜水艇（3）气球（4）飞艇、热气（5）密度计（密度计的刻度是从上到下刻度变大，刻度不均匀，且刻度无单位．）才能正确解答此题．
