题目内容
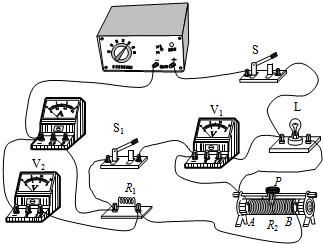 (2011?海淀区二模)如图所示电路,电源两端电压保持不变,闭合开关S,断开开关S1,调节滑动变阻器R2的滑片P使其接入电路的电阻值为其最大值的一半,电压表V1的示数为U1,电流表的示数I1为0.2A;闭合开关S、S1,此时小灯泡L正常发光,电流表的示数I2为0.5A;闭合开关S,断开开关S1,调节滑动变阻器R2滑片P至B端,电压表V2的示数为U2,再调节滑动变阻器R2的滑片P使接入电路的电阻值为其最大值的3/4,此时电路消耗的总功率P为1W.已知5U1=6U2,忽略温度对灯丝电阻的影响.求:
(2011?海淀区二模)如图所示电路,电源两端电压保持不变,闭合开关S,断开开关S1,调节滑动变阻器R2的滑片P使其接入电路的电阻值为其最大值的一半,电压表V1的示数为U1,电流表的示数I1为0.2A;闭合开关S、S1,此时小灯泡L正常发光,电流表的示数I2为0.5A;闭合开关S,断开开关S1,调节滑动变阻器R2滑片P至B端,电压表V2的示数为U2,再调节滑动变阻器R2的滑片P使接入电路的电阻值为其最大值的3/4,此时电路消耗的总功率P为1W.已知5U1=6U2,忽略温度对灯丝电阻的影响.求:(1)电阻R1和灯丝电阻RL的比值;
(2)小灯泡L的额定电功率.
分析:(1)闭合开关S,开关S1断开时,灯泡、R1、接入电路的电阻值为其最大值的一半的滑动变阻器R2串联,V1测灯泡两端的电压;闭合开关S、S1时,电路为灯泡的简单电路;根据欧姆定律求出灯泡两端的电压之比,利用5U1=6U2求出R1和灯泡的电压之比,进一步根据欧姆定律求出电阻R1和灯丝电阻RL的比值.
(2)根据闭合开关S,开关S1断开时,灯泡两端的电压与电阻R1、滑动变阻器两端电压之和的比值,进一步求出滑动变阻器的最大阻值与灯泡电阻的比值;根据电源的电压不变,求出闭合开关S断开开关S1,调节滑动变阻器R2的滑片P使接入电路的电阻值为其最大值的
时电路中的电流;根据电路消耗的总功率和P=UI求出电源的电压,进一步求出小灯泡L的额定电功率.
(2)根据闭合开关S,开关S1断开时,灯泡两端的电压与电阻R1、滑动变阻器两端电压之和的比值,进一步求出滑动变阻器的最大阻值与灯泡电阻的比值;根据电源的电压不变,求出闭合开关S断开开关S1,调节滑动变阻器R2的滑片P使接入电路的电阻值为其最大值的
| 3 |
| 4 |
解答:解:当开关S闭合、S1断开,滑动变阻器R2接入电路电阻为其最大值一半时,电路如图甲所示;当开关S、S1均闭合时,电路如图乙所示;当开关S闭合,断开开关S1,滑动变阻器R2的滑片P在B端时,电路如图丙所示;再调节滑动变阻器R2的滑片P使其接入电路电阻为其最大值
时,电路如图丁所示.
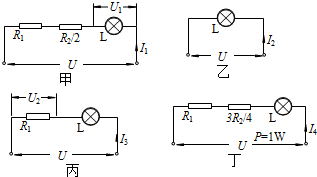
(1)由图甲、乙得:通过的电流分别为I1=0.2A,I2=0.5A,
灯泡两端的电压分别为U1=I1RL,U=I2RL,
电压之比为
=
,
因5U1=6U2,
所以
=
,
由丙图可得:
=
解得:
=
--------------①;
(2)由图甲得:
=
解得:2R1+R2=3RL-------------②
由①②解得:
=
由图乙、丁得:I2RL=I4(R1+
+RL)
解得:I4=
A,
因P=UI4=1W,解得:U=6V,
则P额=UI2=3W.
答:电阻R1和灯丝电阻RL的比值为1:2;小灯泡L的额定电功率为3W.
| 3 |
| 4 |

(1)由图甲、乙得:通过的电流分别为I1=0.2A,I2=0.5A,
灯泡两端的电压分别为U1=I1RL,U=I2RL,
电压之比为
| U1 |
| U |
| 2 |
| 5 |
因5U1=6U2,
所以
| U2 |
| U |
| 1 |
| 3 |
由丙图可得:
| R1 |
| R1+RL |
| 1 |
| 3 |
解得:
| R1 |
| RL |
| 1 |
| 2 |
(2)由图甲得:
| RL | ||
R1+
|
| U1 |
| U-U1 |
解得:2R1+R2=3RL-------------②
由①②解得:
| R2 |
| RL |
| 2 |
| 1 |
由图乙、丁得:I2RL=I4(R1+
| 3R2 |
| 4 |
解得:I4=
| 1 |
| 6 |
因P=UI4=1W,解得:U=6V,
则P额=UI2=3W.
答:电阻R1和灯丝电阻RL的比值为1:2;小灯泡L的额定电功率为3W.
点评:此题是有关欧姆定律、电功率的综合计算题目.在解题过程中,注意电路的分析,根据已知条件分析出各种情况下的等效电路图,同时要注意在串联电路中各物理量之间的关系,结合题目中给出的已知条件进行解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
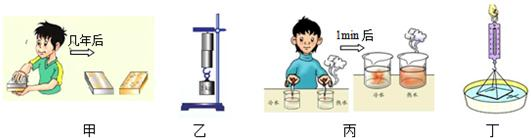
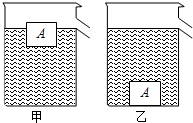 (2011?海淀区二模)将甲、乙两个完全相同的溢水杯放在水平桌面上,甲溢水杯中装满密度为ρ1的液体,乙溢水杯中装满密度为ρ2的液体.如图甲所示,将密度为ρ,重为G 的物块A轻轻放入甲溢水杯中,物块A漂浮在液面上,并且有1/4体积露出液面,液体对甲溢水杯杯底的压强为p1.如图乙所示,将物块A轻轻放入乙溢水杯中,物块A沉底,物块A对乙溢水杯杯底的压力为F,液体对乙溢水杯杯底的压强为p2.已知ρ1:ρ2=3:2,则下列说法中正确的是( )
(2011?海淀区二模)将甲、乙两个完全相同的溢水杯放在水平桌面上,甲溢水杯中装满密度为ρ1的液体,乙溢水杯中装满密度为ρ2的液体.如图甲所示,将密度为ρ,重为G 的物块A轻轻放入甲溢水杯中,物块A漂浮在液面上,并且有1/4体积露出液面,液体对甲溢水杯杯底的压强为p1.如图乙所示,将物块A轻轻放入乙溢水杯中,物块A沉底,物块A对乙溢水杯杯底的压力为F,液体对乙溢水杯杯底的压强为p2.已知ρ1:ρ2=3:2,则下列说法中正确的是( )