题目内容
（2008?青岛模拟）演绎式探究：（1）自由电子在导体中定向移动形成电流．物理学上把单位时间通过导体横截面积的电荷叫电流．若用字母Q表示电荷，用字母t表示通电时间，则电流的定义式为：I=
| Q |
| t |
| Q |
| t |
（2）若流过导体的电流为0.5A，导体中要流过20C的电荷（C为电荷的国际单位库仑），则通电时间为
40
40
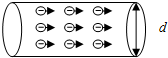
s．（3）若流过导体单位体积的电子个数为n，每个电子所带电荷为e，电子在导体中流动速度为v，导体直径为d，则导体中电流的数学表达式为：I=
| nπevd2 |
| 4 |
| nπevd2 |
| 4 |
分析：（1）根据电流的定义分析答题；
（2）由电流定义式的变形公式分析答题；
（3）已知电子移动的速度，可以求出电子在时间t内移动的距离；已知导体的直径，可以求出导体的横截面积；已知导体中单位体积内电子个数，可以求出时间t内，通过导体横截面的电荷数；已知通过横截面的电荷数和每个电子的电荷量，可以得到一定时间t通过导体横截面的电荷量；已知电荷量和通电时间，根据电流的定义式可以求出电流的数学表达式．
（2）由电流定义式的变形公式分析答题；
（3）已知电子移动的速度，可以求出电子在时间t内移动的距离；已知导体的直径，可以求出导体的横截面积；已知导体中单位体积内电子个数，可以求出时间t内，通过导体横截面的电荷数；已知通过横截面的电荷数和每个电子的电荷量，可以得到一定时间t通过导体横截面的电荷量；已知电荷量和通电时间，根据电流的定义式可以求出电流的数学表达式．
解答：解：（1）时间t内通过导体横截面的电荷量是Q，
根据电流的定义可知，电流I=
．
（2）∵I=
，∴通电时间t=
=
=40s．
（3）t时间内电子移动的距离L=vt，
导体的横截面积S=π(
)2=
，
t时间内通过导体某一横截面的电子数N=nSL=
，
t时间内通过导体某一横截面的电荷量Q=Ne=
，
通过导体的电流I=
=
；
故答案为：（1）
；（2）40；（3）=
．
根据电流的定义可知，电流I=
| Q |
| t |
（2）∵I=
| Q |
| t |
| Q |
| I |
| 20C |
| 0.5A |
（3）t时间内电子移动的距离L=vt，
导体的横截面积S=π(
| d |
| 2 |
| πd2 |
| 4 |
t时间内通过导体某一横截面的电子数N=nSL=
| nπvtd2 |
| 4 |
t时间内通过导体某一横截面的电荷量Q=Ne=
| nπevtd2 |
| 4 |
通过导体的电流I=
| Q |
| t |
| nπevd2 |
| 4 |
故答案为：（1）
| Q |
| t |
| nπevd2 |
| 4 |
点评：本题考查了电流的定义式、求通过一定电量所需要的时间、推导导体中电流的微观表达式，最后一问难度较大，解题时，要认真审题，获取必要的信息，然后解题．
练习册系列答案
相关题目
（2008?青岛模拟）如图所示，木块A紧贴在墙上竖直向下做匀速运动，F为加给它的水平力，下列说法错误的是（ ）